| Codeforces Round 599 (Div. 1) |
|---|
| Finished |
Ujan has finally cleaned up his house and now wants to decorate the interior. He decided to place a beautiful carpet that would really tie the guest room together.
He is interested in carpets that are made up of polygonal patches such that each side of a patch is either a side of another (different) patch, or is an exterior side of the whole carpet. In other words, the carpet can be represented as a planar graph, where each patch corresponds to a face of the graph, each face is a simple polygon. The perimeter of the carpet is the number of the exterior sides.
Ujan considers a carpet beautiful if it consists of $$$f$$$ patches, where the $$$i$$$-th patch has exactly $$$a_i$$$ sides, and the perimeter is the smallest possible. Find an example of such a carpet, so that Ujan can order it!
The first line of input contains a single integer $$$f$$$ ($$$1 \leq f \leq 10^5$$$), the number of patches in the carpet.
The next line contains $$$f$$$ integers $$$a_1, \ldots, a_f$$$ ($$$3 \leq a_i \leq 3\cdot 10^5$$$), the number of sides of the patches. The total number of the sides of the patches $$$a_1 + \ldots + a_f$$$ does not exceed $$$3\cdot10^5$$$.
Output the description of the carpet as a graph.
First, output a single integer $$$n$$$ ($$$3 \leq n \leq 3 \cdot 10^5$$$), the total number of vertices in your graph (the vertices must be numbered from $$$1$$$ to $$$n$$$).
Then output $$$f$$$ lines containing the description of the faces. The $$$i$$$-th line should describe the $$$i$$$-th face and contain $$$a_i$$$ distinct integers $$$v_{i,1}, \ldots, v_{i,a_i}$$$ ($$$1 \leq v_{i,j} \leq n$$$), which means that the vertices $$$v_{i,j}$$$ and $$$v_{i,(j \bmod{a_i})+1}$$$ are connected by an edge for any $$$1 \leq j \leq a_i$$$.
The graph should be planar and satisfy the restrictions described in the problem statement. Its perimeter should be the smallest possible. There should be no double edges or self-loops in the graph. The graph should be connected. Note that a solution always exists; if there are multiple solutions, output any of them.
2 3 3
4 2 1 4 1 2 3
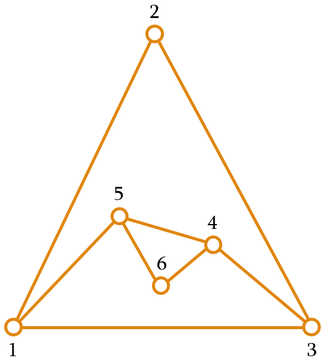
3 5 3 5
6 1 2 3 4 5 4 5 6 1 3 4 6 5
In the first sample, the two triangular faces are connected by a single edge, which results in the minimum perimeter $$$4$$$.
The figure shows one possible configuration for the second sample. The minimum perimeter in this case is $$$3$$$.
| Name |
|---|




