| Codeforces Round 592 (Div. 2) |
|---|
| Finished |
There are $$$n$$$ chips arranged in a circle, numbered from $$$1$$$ to $$$n$$$.
Initially each chip has black or white color. Then $$$k$$$ iterations occur. During each iteration the chips change their colors according to the following rules. For each chip $$$i$$$, three chips are considered: chip $$$i$$$ itself and two its neighbours. If the number of white chips among these three is greater than the number of black chips among these three chips, then the chip $$$i$$$ becomes white. Otherwise, the chip $$$i$$$ becomes black.
Note that for each $$$i$$$ from $$$2$$$ to $$$(n - 1)$$$ two neighbouring chips have numbers $$$(i - 1)$$$ and $$$(i + 1)$$$. The neighbours for the chip $$$i = 1$$$ are $$$n$$$ and $$$2$$$. The neighbours of $$$i = n$$$ are $$$(n - 1)$$$ and $$$1$$$.
The following picture describes one iteration with $$$n = 6$$$. The chips $$$1$$$, $$$3$$$ and $$$4$$$ are initially black, and the chips $$$2$$$, $$$5$$$ and $$$6$$$ are white. After the iteration $$$2$$$, $$$3$$$ and $$$4$$$ become black, and $$$1$$$, $$$5$$$ and $$$6$$$ become white.
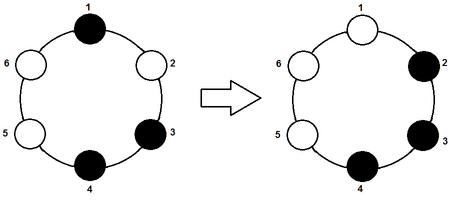
Your task is to determine the color of each chip after $$$k$$$ iterations.
The first line contains two integers $$$n$$$ and $$$k$$$ $$$(3 \le n \le 200\,000, 1 \le k \le 10^{9})$$$ — the number of chips and the number of iterations, respectively.
The second line contains a string consisting of $$$n$$$ characters "W" and "B". If the $$$i$$$-th character is "W", then the $$$i$$$-th chip is white initially. If the $$$i$$$-th character is "B", then the $$$i$$$-th chip is black initially.
Print a string consisting of $$$n$$$ characters "W" and "B". If after $$$k$$$ iterations the $$$i$$$-th chip is white, then the $$$i$$$-th character should be "W". Otherwise the $$$i$$$-th character should be "B".
6 1 BWBBWW
WBBBWW
7 3 WBWBWBW
WWWWWWW
6 4 BWBWBW
BWBWBW
The first example is described in the statement.
The second example: "WBWBWBW" $$$\rightarrow$$$ "WWBWBWW" $$$\rightarrow$$$ "WWWBWWW" $$$\rightarrow$$$ "WWWWWWW". So all chips become white.
The third example: "BWBWBW" $$$\rightarrow$$$ "WBWBWB" $$$\rightarrow$$$ "BWBWBW" $$$\rightarrow$$$ "WBWBWB" $$$\rightarrow$$$ "BWBWBW".
| Name |
|---|




