| Codeforces Round 612 (Div. 1) |
|---|
| Finished |
Evlampiy was gifted a rooted tree. The vertices of the tree are numbered from $$$1$$$ to $$$n$$$. Each of its vertices also has an integer $$$a_i$$$ written on it. For each vertex $$$i$$$, Evlampiy calculated $$$c_i$$$ — the number of vertices $$$j$$$ in the subtree of vertex $$$i$$$, such that $$$a_j < a_i$$$.
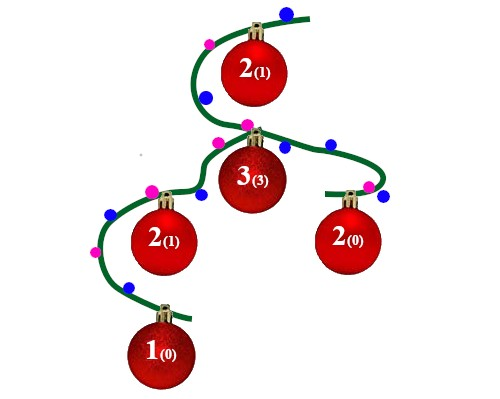 Illustration for the second example, the first integer is $$$a_i$$$ and the integer in parentheses is $$$c_i$$$
Illustration for the second example, the first integer is $$$a_i$$$ and the integer in parentheses is $$$c_i$$$After the new year, Evlampiy could not remember what his gift was! He remembers the tree and the values of $$$c_i$$$, but he completely forgot which integers $$$a_i$$$ were written on the vertices.
Help him to restore initial integers!
The first line contains an integer $$$n$$$ $$$(1 \leq n \leq 2000)$$$ — the number of vertices in the tree.
The next $$$n$$$ lines contain descriptions of vertices: the $$$i$$$-th line contains two integers $$$p_i$$$ and $$$c_i$$$ ($$$0 \leq p_i \leq n$$$; $$$0 \leq c_i \leq n-1$$$), where $$$p_i$$$ is the parent of vertex $$$i$$$ or $$$0$$$ if vertex $$$i$$$ is root, and $$$c_i$$$ is the number of vertices $$$j$$$ in the subtree of vertex $$$i$$$, such that $$$a_j < a_i$$$.
It is guaranteed that the values of $$$p_i$$$ describe a rooted tree with $$$n$$$ vertices.
If a solution exists, in the first line print "YES", and in the second line output $$$n$$$ integers $$$a_i$$$ $$$(1 \leq a_i \leq {10}^{9})$$$. If there are several solutions, output any of them. One can prove that if there is a solution, then there is also a solution in which all $$$a_i$$$ are between $$$1$$$ and $$$10^9$$$.
If there are no solutions, print "NO".
3 2 0 0 2 2 0
YES 1 2 1
5 0 1 1 3 2 1 3 0 2 0
YES 2 3 2 1 2
| Name |
|---|




