| Codeforces Round 618 (Div. 1) |
|---|
| Finished |
Guy-Manuel and Thomas are planning $$$144$$$ trips around the world.
You are given a simple weighted undirected connected graph with $$$n$$$ vertexes and $$$m$$$ edges with the following restriction: there isn't any simple cycle (i. e. a cycle which doesn't pass through any vertex more than once) of length greater than $$$3$$$ which passes through the vertex $$$1$$$. The cost of a path (not necessarily simple) in this graph is defined as the XOR of weights of all edges in that path with each edge being counted as many times as the path passes through it.
But the trips with cost $$$0$$$ aren't exciting.
You may choose any subset of edges incident to the vertex $$$1$$$ and remove them. How many are there such subsets, that, when removed, there is not any nontrivial cycle with the cost equal to $$$0$$$ which passes through the vertex $$$1$$$ in the resulting graph? A cycle is called nontrivial if it passes through some edge odd number of times. As the answer can be very big, output it modulo $$$10^9+7$$$.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n,m \le 10^5$$$) — the number of vertexes and edges in the graph. The $$$i$$$-th of the next $$$m$$$ lines contains three integers $$$a_i$$$, $$$b_i$$$ and $$$w_i$$$ ($$$1 \le a_i, b_i \le n, a_i \neq b_i, 0 \le w_i < 32$$$) — the endpoints of the $$$i$$$-th edge and its weight. It's guaranteed there aren't any multiple edges, the graph is connected and there isn't any simple cycle of length greater than $$$3$$$ which passes through the vertex $$$1$$$.
Output the answer modulo $$$10^9+7$$$.
6 8 1 2 0 2 3 1 2 4 3 2 6 2 3 4 8 3 5 4 5 4 5 5 6 6
2
7 9 1 2 0 1 3 1 2 3 9 2 4 3 2 5 4 4 5 7 3 6 6 3 7 7 6 7 8
1
4 4 1 2 27 1 3 1 1 4 1 3 4 0
6
The pictures below represent the graphs from examples. 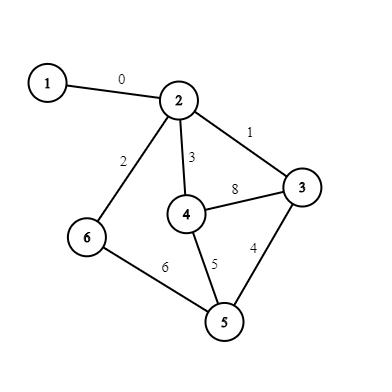 In the first example, there aren't any nontrivial cycles with cost $$$0$$$, so we can either remove or keep the only edge incident to the vertex $$$1$$$.
In the first example, there aren't any nontrivial cycles with cost $$$0$$$, so we can either remove or keep the only edge incident to the vertex $$$1$$$. 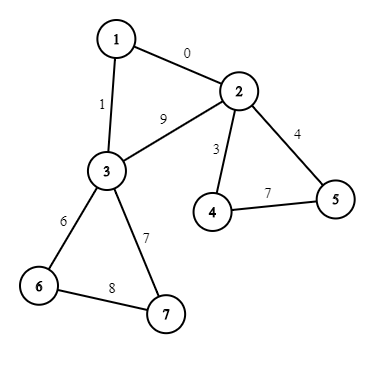 In the second example, if we don't remove the edge $$$1-2$$$, then there is a cycle $$$1-2-4-5-2-1$$$ with cost $$$0$$$; also if we don't remove the edge $$$1-3$$$, then there is a cycle $$$1-3-2-4-5-2-3-1$$$ of cost $$$0$$$. The only valid subset consists of both edges.
In the second example, if we don't remove the edge $$$1-2$$$, then there is a cycle $$$1-2-4-5-2-1$$$ with cost $$$0$$$; also if we don't remove the edge $$$1-3$$$, then there is a cycle $$$1-3-2-4-5-2-3-1$$$ of cost $$$0$$$. The only valid subset consists of both edges. 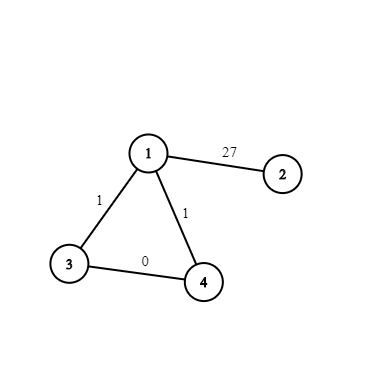 In the third example, all subsets are valid except for those two in which both edges $$$1-3$$$ and $$$1-4$$$ are kept.
In the third example, all subsets are valid except for those two in which both edges $$$1-3$$$ and $$$1-4$$$ are kept.
| Name |
|---|




