| Codeforces Round 624 (Div. 3) |
|---|
| Finished |
You are given two integers $$$n$$$ and $$$d$$$. You need to construct a rooted binary tree consisting of $$$n$$$ vertices with a root at the vertex $$$1$$$ and the sum of depths of all vertices equals to $$$d$$$.
A tree is a connected graph without cycles. A rooted tree has a special vertex called the root. A parent of a vertex $$$v$$$ is the last different from $$$v$$$ vertex on the path from the root to the vertex $$$v$$$. The depth of the vertex $$$v$$$ is the length of the path from the root to the vertex $$$v$$$. Children of vertex $$$v$$$ are all vertices for which $$$v$$$ is the parent. The binary tree is such a tree that no vertex has more than $$$2$$$ children.
You have to answer $$$t$$$ independent test cases.
The first line of the input contains one integer $$$t$$$ ($$$1 \le t \le 1000$$$) — the number of test cases.
The only line of each test case contains two integers $$$n$$$ and $$$d$$$ ($$$2 \le n, d \le 5000$$$) — the number of vertices in the tree and the required sum of depths of all vertices.
It is guaranteed that the sum of $$$n$$$ and the sum of $$$d$$$ both does not exceed $$$5000$$$ ($$$\sum n \le 5000, \sum d \le 5000$$$).
For each test case, print the answer.
If it is impossible to construct such a tree, print "NO" (without quotes) in the first line. Otherwise, print "{YES}" in the first line. Then print $$$n-1$$$ integers $$$p_2, p_3, \dots, p_n$$$ in the second line, where $$$p_i$$$ is the parent of the vertex $$$i$$$. Note that the sequence of parents you print should describe some binary tree.
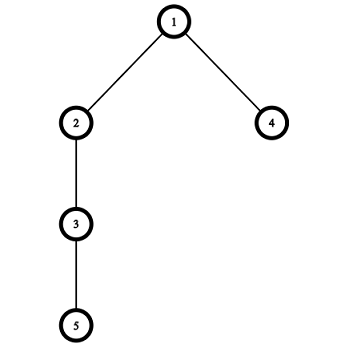
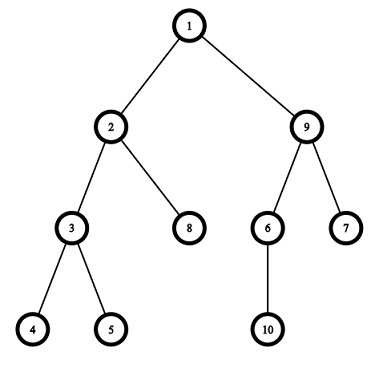
3 5 7 10 19 10 18
YES 1 2 1 3 YES 1 2 3 3 9 9 2 1 6 NO
Pictures corresponding to the first and the second test cases of the example:
| Name |
|---|




