| CodeCraft-20 (Div. 2) |
|---|
| Finished |
Nash designed an interesting yet simple board game where a player is simply required to follow instructions written on the cell where the player currently stands.
This board game is played on the $$$n\times n$$$ board. Rows and columns of this board are numbered from $$$1$$$ to $$$n$$$. The cell on the intersection of the $$$r$$$-th row and $$$c$$$-th column is denoted by $$$(r, c)$$$.
Some cells on the board are called blocked zones. On each cell of the board, there is written one of the following $$$5$$$ characters — $$$U$$$, $$$D$$$, $$$L$$$, $$$R$$$ or $$$X$$$ — instructions for the player. Suppose that the current cell is $$$(r, c)$$$. If the character is $$$R$$$, the player should move to the right cell $$$(r, c+1)$$$, for $$$L$$$ the player should move to the left cell $$$(r, c-1)$$$, for $$$U$$$ the player should move to the top cell $$$(r-1, c)$$$, for $$$D$$$ the player should move to the bottom cell $$$(r+1, c)$$$. Finally, if the character in the cell is $$$X$$$, then this cell is the blocked zone. The player should remain in this cell (the game for him isn't very interesting from now on).
It is guaranteed that the characters are written in a way that the player will never have to step outside of the board, no matter at which cell he starts.
As a player starts from a cell, he moves according to the character in the current cell. The player keeps moving until he lands in a blocked zone. It is also possible that the player will keep moving infinitely long.
For every of the $$$n^2$$$ cells of the board Alice, your friend, wants to know, how will the game go, if the player starts in this cell. For each starting cell of the board, she writes down the cell that the player stops at, or that the player never stops at all. She gives you the information she has written: for each cell $$$(r, c)$$$ she wrote:
- a pair ($$$x$$$,$$$y$$$), meaning if a player had started at $$$(r, c)$$$, he would end up at cell ($$$x$$$,$$$y$$$).
- or a pair ($$$-1$$$,$$$-1$$$), meaning if a player had started at $$$(r, c)$$$, he would keep moving infinitely long and would never enter the blocked zone.
It might be possible that Alice is trying to fool you and there's no possible grid that satisfies all the constraints Alice gave you. For the given information Alice provided you, you are required to decipher a possible board, or to determine that such a board doesn't exist. If there exist several different boards that satisfy the provided information, you can find any of them.
The first line of the input contains a single integer $$$n$$$ ($$$1 \leq n \leq 10^{3}$$$) — the side of the board.
The $$$i$$$-th of the next $$$n$$$ lines of the input contains $$$2n$$$ integers $$$x_1, y_1, x_2, y_2, \dots, x_n, y_n$$$, where $$$(x_j, y_j)$$$ ($$$1 \leq x_j \leq n, 1 \leq y_j \leq n$$$, or $$$(x_j,y_j)=(-1,-1)$$$) is the pair written by Alice for the cell $$$(i, j)$$$.
If there doesn't exist a board satisfying the information that Alice gave you, print a single line containing INVALID.
Otherwise, in the first line print VALID. In the $$$i$$$-th of the next $$$n$$$ lines, print the string of $$$n$$$ characters, corresponding to the characters in the $$$i$$$-th row of the suitable board you found. Each character of a string can either be $$$U$$$, $$$D$$$, $$$L$$$, $$$R$$$ or $$$X$$$. If there exist several different boards that satisfy the provided information, you can find any of them.
2 1 1 1 1 2 2 2 2
VALID XL RX
3 -1 -1 -1 -1 -1 -1 -1 -1 2 2 -1 -1 -1 -1 -1 -1 -1 -1
VALID RRD UXD ULL
For the sample test 1 :
The given grid in output is a valid one.
- If the player starts at $$$(1,1)$$$, he doesn't move any further following $$$X$$$ and stops there.
- If the player starts at $$$(1,2)$$$, he moves to left following $$$L$$$ and stops at $$$(1,1)$$$.
- If the player starts at $$$(2,1)$$$, he moves to right following $$$R$$$ and stops at $$$(2,2)$$$.
- If the player starts at $$$(2,2)$$$, he doesn't move any further following $$$X$$$ and stops there.
The simulation can be seen below :
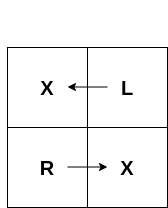
For the sample test 2 :
The given grid in output is a valid one, as a player starting at any cell other than the one at center $$$(2,2)$$$, keeps moving in an infinitely long cycle and never stops. Had he started at $$$(2,2)$$$, he wouldn't have moved further following instruction $$$X$$$ .
The simulation can be seen below :
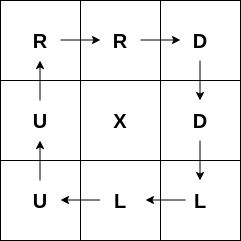
| Name |
|---|




