| Codeforces Round 627 (Div. 3) |
|---|
| Finished |
There is a frog staying to the left of the string $$$s = s_1 s_2 \ldots s_n$$$ consisting of $$$n$$$ characters (to be more precise, the frog initially stays at the cell $$$0$$$). Each character of $$$s$$$ is either 'L' or 'R'. It means that if the frog is staying at the $$$i$$$-th cell and the $$$i$$$-th character is 'L', the frog can jump only to the left. If the frog is staying at the $$$i$$$-th cell and the $$$i$$$-th character is 'R', the frog can jump only to the right. The frog can jump only to the right from the cell $$$0$$$.
Note that the frog can jump into the same cell twice and can perform as many jumps as it needs.
The frog wants to reach the $$$n+1$$$-th cell. The frog chooses some positive integer value $$$d$$$ before the first jump (and cannot change it later) and jumps by no more than $$$d$$$ cells at once. I.e. if the $$$i$$$-th character is 'L' then the frog can jump to any cell in a range $$$[max(0, i - d); i - 1]$$$, and if the $$$i$$$-th character is 'R' then the frog can jump to any cell in a range $$$[i + 1; min(n + 1; i + d)]$$$.
The frog doesn't want to jump far, so your task is to find the minimum possible value of $$$d$$$ such that the frog can reach the cell $$$n+1$$$ from the cell $$$0$$$ if it can jump by no more than $$$d$$$ cells at once. It is guaranteed that it is always possible to reach $$$n+1$$$ from $$$0$$$.
You have to answer $$$t$$$ independent test cases.
The first line of the input contains one integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
The next $$$t$$$ lines describe test cases. The $$$i$$$-th test case is described as a string $$$s$$$ consisting of at least $$$1$$$ and at most $$$2 \cdot 10^5$$$ characters 'L' and 'R'.
It is guaranteed that the sum of lengths of strings over all test cases does not exceed $$$2 \cdot 10^5$$$ ($$$\sum |s| \le 2 \cdot 10^5$$$).
For each test case, print the answer — the minimum possible value of $$$d$$$ such that the frog can reach the cell $$$n+1$$$ from the cell $$$0$$$ if it jumps by no more than $$$d$$$ at once.
6 LRLRRLL L LLR RRRR LLLLLL R
3 2 3 1 7 1
The picture describing the first test case of the example and one of the possible answers:
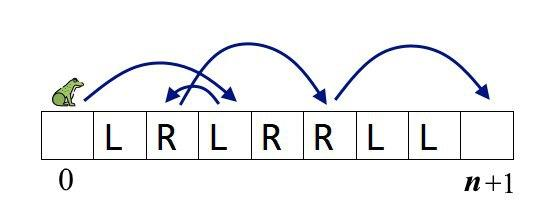
In the second test case of the example, the frog can only jump directly from $$$0$$$ to $$$n+1$$$.
In the third test case of the example, the frog can choose $$$d=3$$$, jump to the cell $$$3$$$ from the cell $$$0$$$ and then to the cell $$$4$$$ from the cell $$$3$$$.
In the fourth test case of the example, the frog can choose $$$d=1$$$ and jump $$$5$$$ times to the right.
In the fifth test case of the example, the frog can only jump directly from $$$0$$$ to $$$n+1$$$.
In the sixth test case of the example, the frog can choose $$$d=1$$$ and jump $$$2$$$ times to the right.
| Name |
|---|




