| Codeforces Round 628 (Div. 2) |
|---|
| Finished |
It's the year 5555. You have a graph, and you want to find a long cycle and a huge independent set, just because you can. But for now, let's just stick with finding either.
Given a connected graph with $$$n$$$ vertices, you can choose to either:
- find an independent set that has exactly $$$\lceil\sqrt{n}\rceil$$$ vertices.
- find a simple cycle of length at least $$$\lceil\sqrt{n}\rceil$$$.
An independent set is a set of vertices such that no two of them are connected by an edge. A simple cycle is a cycle that doesn't contain any vertex twice. I have a proof you can always solve one of these problems, but it's too long to fit this margin.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$5 \le n \le 10^5$$$, $$$n-1 \le m \le 2 \cdot 10^5$$$) — the number of vertices and edges in the graph.
Each of the next $$$m$$$ lines contains two space-separated integers $$$u$$$ and $$$v$$$ ($$$1 \le u,v \le n$$$) that mean there's an edge between vertices $$$u$$$ and $$$v$$$. It's guaranteed that the graph is connected and doesn't contain any self-loops or multiple edges.
If you choose to solve the first problem, then on the first line print "1", followed by a line containing $$$\lceil\sqrt{n}\rceil$$$ distinct integers not exceeding $$$n$$$, the vertices in the desired independent set.
If you, however, choose to solve the second problem, then on the first line print "2", followed by a line containing one integer, $$$c$$$, representing the length of the found cycle, followed by a line containing $$$c$$$ distinct integers integers not exceeding $$$n$$$, the vertices in the desired cycle, in the order they appear in the cycle.
6 6 1 3 3 4 4 2 2 6 5 6 5 1
1 1 6 4
6 8 1 3 3 4 4 2 2 6 5 6 5 1 1 4 2 5
2 4 1 5 2 4
5 4 1 2 1 3 2 4 2 5
1 3 4 5
In the first sample:
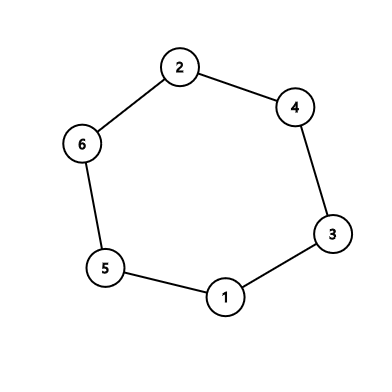
Notice that you can solve either problem, so printing the cycle $$$2-4-3-1-5-6$$$ is also acceptable.
In the second sample:
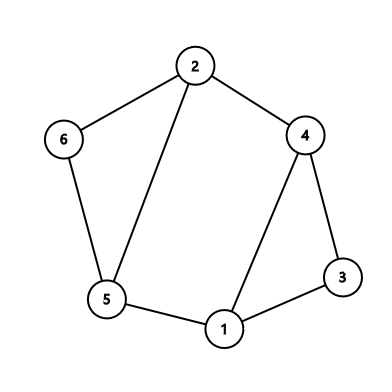
Notice that if there are multiple answers you can print any, so printing the cycle $$$2-5-6$$$, for example, is acceptable.
In the third sample:
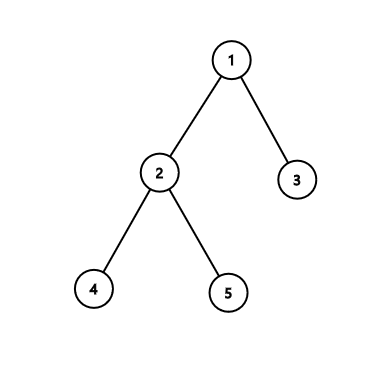
| Name |
|---|




