| Codeforces Round 633 (Div. 1) |
|---|
| Finished |
Due to the success of TWICE, JYP Entertainment has earned countless money and emerged as the biggest entertainment firm by market capitalization. Therefore, the boss, JYP, has decided to create a new nation and has appointed you to provide a design diagram.
The new nation consists of $$$n$$$ cities and some roads between them. JYP has given some restrictions:
- To guarantee efficiency while avoiding chaos, for any $$$2$$$ different cities $$$A$$$ and $$$B$$$, there is exactly one road between them, and it is one-directional. There are no roads connecting a city to itself.
- The logo of rivaling companies should not appear in the plan, that is, there does not exist $$$4$$$ distinct cities $$$A$$$,$$$B$$$,$$$C$$$,$$$D$$$ , such that the following configuration occurs.
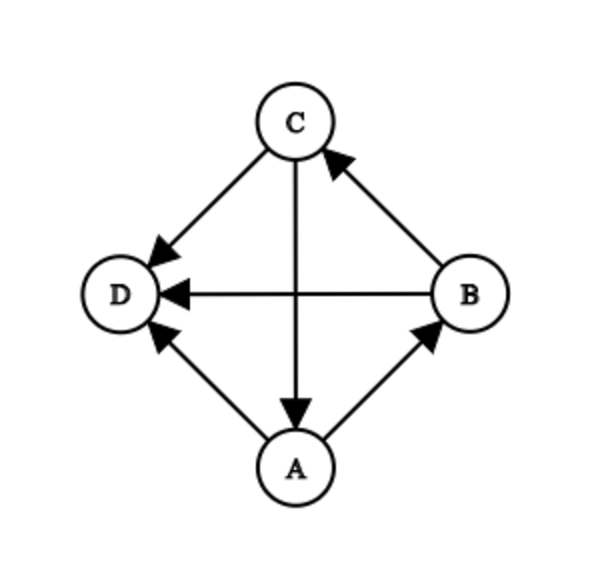
JYP has given criteria for your diagram. For two cities $$$A$$$,$$$B$$$, let $$$dis(A,B)$$$ be the smallest number of roads you have to go through to get from $$$A$$$ to $$$B$$$. If it is not possible to walk from $$$A$$$ to $$$B$$$, $$$dis(A,B) = 614n$$$. Then, the efficiency value is defined to be the sum of $$$dis(A,B)$$$ for all ordered pairs of distinct cities $$$(A,B)$$$.
Note that $$$dis(A,B)$$$ doesn't have to be equal to $$$dis(B,A)$$$.
You have drawn a design diagram that satisfies JYP's restrictions. Find the sum of $$$dis(A,B)$$$ over all ordered pairs of cities $$$(A,B)$$$ with $$$A\neq B$$$.
Note that the input is given in compressed form. But even though it is compressed, you'd better use fast input.
The first line contains a single integer $$$n$$$ ($$$4 \le n \le 8000$$$, $$$n \equiv 0 \pmod{4}$$$) — the number of cities.
A binary matrix is encrypted in the following format. Each of $$$n$$$ next lines contains $$$\frac{n}{4}$$$ one-digit hexadecimal numbers (that is, these numbers can be represented either as digits from $$$0$$$ to $$$9$$$ or as uppercase Latin letters from $$$A$$$ to $$$F$$$). Binary representation of each of these numbers denotes next $$$4$$$ elements of the matrix in the corresponding row. For example, if the number $$$B$$$ is given, then the corresponding elements are $$$1011$$$, and if the number is $$$5$$$, then the corresponding elements are $$$0101$$$.
After you obtain the decrypted binary matrix, the $$$j$$$-th character of the $$$i$$$-th row is $$$1$$$ if the one-directional road between cities $$$i$$$ and $$$j$$$ is directed from $$$i$$$ to $$$j$$$, and $$$0$$$ otherwise. It is guaranteed that the graph satisfies the restrictions mentioned above.
Output one integer, representing the sum of $$$dis(A,B)$$$ over all ordered pairs of cities $$$(A,B)$$$ with $$$A\neq B$$$.
4 7 2 1 4
7380
8 7F 3F 1F 0C 06 03 11 18
88464
The first example corresponds to the matrix:
$$$\begin{matrix} 0111 \\ 0010 \\ 0001 \\ 0100 \\ \end{matrix}$$$
Which corresponds to this graph:

$$$dis(1,2)=dis(1,3)=dis(1,4)=dis(2,3)=dis(3,4)=dis(4,2)=1$$$
$$$dis(2,4)=dis(4,3)=dis(3,2)=2$$$
$$$dis(2,1)=dis(3,1)=dis(4,1)=2456$$$
Therefore the answer for the diagram is $$$7380$$$.
| Name |
|---|




