| Codeforces Round 650 (Div. 3) |
|---|
| Закончено |
В магазине продаются $$$n$$$ бусинок. Цвет каждой бусинки описывается строчной буквой латинского алфавита («a»–«z»). Вы хотите купить какие-то бусинки, чтобы собрать из них ожерелье.
Ожерелье — набор бусинок, соединенных по кругу.
Например, если в магазине продаются бусинки «a», «b», «c», «a», «c», «c», то вы можете собрать следующие ожерелья (это не все возможные варианты):
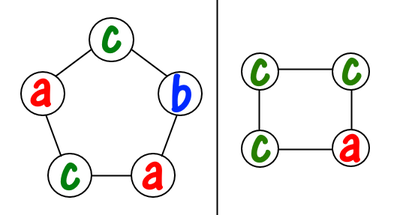
А следующие ожерелья нельзя собрать из бусинок, которые продаются в магазине:
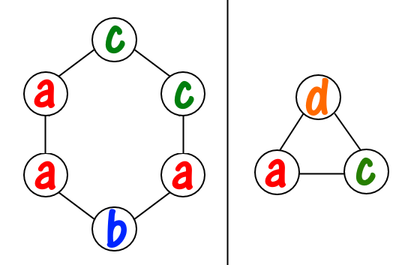 Первое ожерелье собрать не получится, потому что в нем есть три бусинки «a» (из двух доступных). Второе ожерелье собрать не получится, потому что в нем есть бусинка «d», которой нет в магазине.
Первое ожерелье собрать не получится, потому что в нем есть три бусинки «a» (из двух доступных). Второе ожерелье собрать не получится, потому что в нем есть бусинка «d», которой нет в магазине. Назовем ожерелье $$$k$$$-красивым, если при его повороте по часовой стрелке на $$$k$$$ бусинок ожерелье остается неизменным. Например, вот последовательность из трех поворотов некоторого ожерелья.
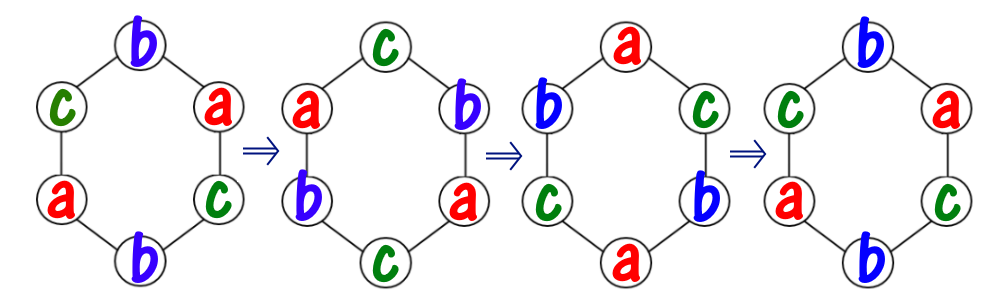
Так как после трех поворотов по часовой стрелке ожерелье не изменилось, то оно является $$$3$$$-красивым. Как можно заметить, это ожерелье также является $$$6$$$-красивым, $$$9$$$-красивым и так далее, но не является $$$1$$$-красивым или $$$2$$$-красивым.
В частности, ожерелье длины $$$1$$$ является $$$k$$$-красивым для любого целого $$$k$$$. Ожерелье, которое состоит из бусинок одинакового цвета, тоже является красивым для любого $$$k$$$.
Вам даны числа $$$n$$$ и $$$k$$$, а также строка $$$s$$$, содержащая $$$n$$$ строчных букв латинского алфавита — каждая буква задает бусинку в магазине. Вы можете купить любое подмножество бусинок и соединить их в произвольном порядке. Найдите максимальную длину $$$k$$$-красивого ожерелья, которое вы можете собрать.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов тестовых данных в тесте. Далее следуют $$$t$$$ наборов тестовых данных.
Первая строка каждого набора содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n, k \le 2000$$$).
Вторая строка каждого набора содержит строку $$$s$$$, содержащую $$$n$$$ строчных букв латинского алфавита — набор бусинок в магазине.
Гарантируется, что сумма $$$n$$$ по всем наборам тестовых данных в тесте не превосходит $$$2000$$$.
Выведите $$$t$$$ ответов на наборы тестовых данных. Каждый ответ является целым положительным числом — максимальной длиной $$$k$$$-красивого ожерелья, которое вы можете собрать.
6 6 3 abcbac 3 6 aaa 7 1000 abczgyo 5 4 ababa 20 10 aaebdbabdbbddaadaadc 20 5 ecbedececacbcbccbdec
6 3 5 4 15 10
Первый набор тестовых данных разобран в условии.
Во втором наборе тестовых данных $$$6$$$-красивое ожерелье можно собрать из всех букв.
В третьем наборе тестовых данных $$$1000$$$-красивое ожерельем можно собрать, например, из бусинок «abzyo».
| Название |
|---|




