| Codeforces Round 652 (Div. 2) |
|---|
| Закончено |
Ли собирается украсить свой дом к вечеринке с помощью нескольких правильных многоугольников...
Ли считает правильный (выпуклый) $$$n$$$-угольник красивым тогда и только тогда, когда он может повернуть многоугольник таким образом, чтобы хотя бы одна из его сторон стала параллельна оси $$$OX$$$ и хотя бы одна из его сторон стала параллельна оси $$$OY$$$ одновременно.
Напомним, что правильный $$$n$$$-угольник — это выпуклый многоугольник из $$$n$$$ вершин такой, что все его стороны и углы равны.
Ли пришел в магазин: в магазине продаются $$$t$$$ правильных многоугольников. Для каждого из них выведите YES, если многоугольник красивый, или NO в противном случае.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество многоугольников в магазине.
В каждой из следующих $$$t$$$ строк задано по одному целому числу $$$n_i$$$ ($$$3 \le n_i \le 10^9$$$): то есть $$$i$$$-й многоугольник является правильным $$$n_i$$$-угольником.
Для каждого многоугольника в магазине, выведите YES, если он красивый, или NO в противном случае (регистр букв не важен).
4 3 4 12 1000000000
NO YES YES YES
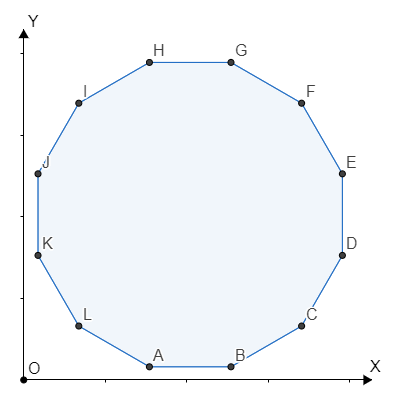
В примере, в магазине продаются $$$4$$$ многоугольника. Несложно определить, что равносторонний треугольник (правильный $$$3$$$-угольник) не является красивым, квадрат (правильный $$$4$$$-угольник) является красивым, и правильный $$$12$$$-угольник (изображен ниже) также является красивым.
| Название |
|---|




