Let $$$a$$$ and $$$b$$$ be some non-negative integers. Let's define strange addition of $$$a$$$ and $$$b$$$ as following:
- write down the numbers one under another and align them by their least significant digit;
- add them up digit by digit and concatenate the respective sums together.
Assume that both numbers have an infinite number of leading zeros.
For example, let's take a look at a strange addition of numbers $$$3248$$$ and $$$908$$$:
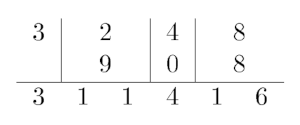
You are given a string $$$c$$$, consisting of $$$n$$$ digits from $$$0$$$ to $$$9$$$. You are also given $$$m$$$ updates of form:
- $$$x~d$$$ — replace the digit at the $$$x$$$-th position of $$$c$$$ with a digit $$$d$$$.
Note that string $$$c$$$ might have leading zeros at any point of time.
After each update print the number of pairs $$$(a, b)$$$ such that both $$$a$$$ and $$$b$$$ are non-negative integers and the result of a strange addition of $$$a$$$ and $$$b$$$ is equal to $$$c$$$.
Note that the numbers of pairs can be quite large, so print them modulo $$$998244353$$$.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 5 \cdot 10^5$$$) — the length of the number $$$c$$$ and the number of updates.
The second line contains a string $$$c$$$, consisting of exactly $$$n$$$ digits from $$$0$$$ to $$$9$$$.
Each of the next $$$m$$$ lines contains two integers $$$x$$$ and $$$d$$$ ($$$1 \le x \le n$$$, $$$0 \le d \le 9$$$) — the descriptions of updates.
Print $$$m$$$ integers — the $$$i$$$-th value should be equal to the number of pairs $$$(a, b)$$$ such that both $$$a$$$ and $$$b$$$ are non-negative integers and the result of a strange addition of $$$a$$$ and $$$b$$$ is equal to $$$c$$$ after $$$i$$$ updates are applied.
Note that the numbers of pairs can be quite large, so print them modulo $$$998244353$$$.
2 3 14 2 4 2 1 1 0
15 12 2
After the first update $$$c$$$ is equal to $$$14$$$. The pairs that sum up to $$$14$$$ are: $$$(0, 14)$$$, $$$(1, 13)$$$, $$$(2, 12)$$$, $$$(3, 11)$$$, $$$(4, 10)$$$, $$$(5, 9)$$$, $$$(6, 8)$$$, $$$(7, 7)$$$, $$$(8, 6)$$$, $$$(9, 5)$$$, $$$(10, 4)$$$, $$$(11, 3)$$$, $$$(12, 2)$$$, $$$(13, 1)$$$, $$$(14, 0)$$$.
After the second update $$$c$$$ is equal to $$$11$$$.
After the third update $$$c$$$ is equal to $$$01$$$.
| Name |
|---|




