| Codeforces Round 662 (Div. 2) |
|---|
| Finished |
Carousel Boutique is busy again! Rarity has decided to visit the pony ball and she surely needs a new dress, because going out in the same dress several times is a sign of bad manners. First of all, she needs a dress pattern, which she is going to cut out from the rectangular piece of the multicolored fabric.
The piece of the multicolored fabric consists of $$$n \times m$$$ separate square scraps. Since Rarity likes dresses in style, a dress pattern must only include scraps sharing the same color. A dress pattern must be the square, and since Rarity is fond of rhombuses, the sides of a pattern must form a $$$45^{\circ}$$$ angle with sides of a piece of fabric (that way it will be resembling the traditional picture of a rhombus).
Examples of proper dress patterns: 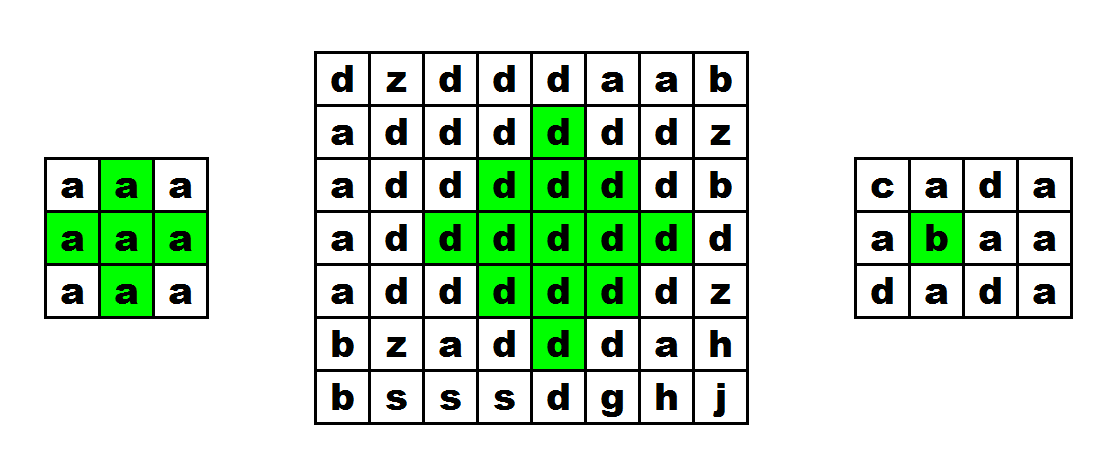 Examples of improper dress patterns:
Examples of improper dress patterns:  The first one consists of multi-colored scraps, the second one goes beyond the bounds of the piece of fabric, the third one is not a square with sides forming a $$$45^{\circ}$$$ angle with sides of the piece of fabric.
The first one consists of multi-colored scraps, the second one goes beyond the bounds of the piece of fabric, the third one is not a square with sides forming a $$$45^{\circ}$$$ angle with sides of the piece of fabric.
Rarity wonders how many ways to cut out a dress pattern that satisfies all the conditions that do exist. Please help her and satisfy her curiosity so she can continue working on her new masterpiece!
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 2000$$$). Each of the next $$$n$$$ lines contains $$$m$$$ characters: lowercase English letters, the $$$j$$$-th of which corresponds to scrap in the current line and in the $$$j$$$-th column. Scraps having the same letter share the same color, scraps having different letters have different colors.
Print a single integer: the number of ways to cut out a dress pattern to satisfy all of Rarity's conditions.
3 3 aaa aaa aaa
10
3 4 abab baba abab
12
5 5 zbacg baaac aaaaa eaaad weadd
31
In the first example, all the dress patterns of size $$$1$$$ and one of size $$$2$$$ are satisfactory.
In the second example, only the dress patterns of size $$$1$$$ are satisfactory.
| Name |
|---|




