| Codeforces Round 664 (Div. 1) |
|---|
| Finished |
No matter what trouble you're in, don't be afraid, but face it with a smile.
I've made another billion dollars!
— Boboniu
Boboniu has issued his currencies, named Bobo Yuan. Bobo Yuan (BBY) is a series of currencies. Boboniu gives each of them a positive integer identifier, such as BBY-1, BBY-2, etc.
Boboniu has a BBY collection. His collection looks like a sequence. For example:

We can use sequence $$$a=[1,2,3,3,2,1,4,4,1]$$$ of length $$$n=9$$$ to denote it.
Now Boboniu wants to fold his collection. You can imagine that Boboniu stick his collection to a long piece of paper and fold it between currencies:
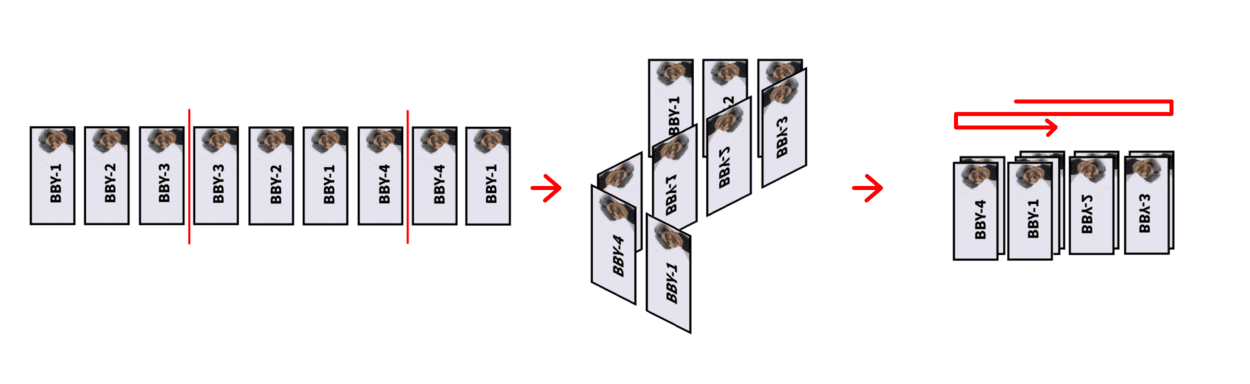
Boboniu will only fold the same identifier of currencies together. In other words, if $$$a_i$$$ is folded over $$$a_j$$$ ($$$1\le i,j\le n$$$), then $$$a_i=a_j$$$ must hold. Boboniu doesn't care if you follow this rule in the process of folding. But once it is finished, the rule should be obeyed.
A formal definition of fold is described in notes.
According to the picture above, you can fold $$$a$$$ two times. In fact, you can fold $$$a=[1,2,3,3,2,1,4,4,1]$$$ at most two times. So the maximum number of folds of it is $$$2$$$.
As an international fan of Boboniu, you're asked to calculate the maximum number of folds.
You're given a sequence $$$a$$$ of length $$$n$$$, for each $$$i$$$ ($$$1\le i\le n$$$), you need to calculate the maximum number of folds of $$$[a_1,a_2,\ldots,a_i]$$$.
The first line contains an integer $$$n$$$ ($$$1\le n\le 10^5$$$).
The second line contains $$$n$$$ integers $$$a_1,a_2,\ldots,a_n$$$ ($$$1\le a_i\le n$$$).
Print $$$n$$$ integers. The $$$i$$$-th of them should be equal to the maximum number of folds of $$$[a_1,a_2,\ldots,a_i]$$$.
9 1 2 3 3 2 1 4 4 1
0 0 0 1 1 1 1 2 2
9 1 2 2 2 2 1 1 2 2
0 0 1 2 3 3 4 4 5
15 1 2 3 4 5 5 4 3 2 2 3 4 4 3 6
0 0 0 0 0 1 1 1 1 2 2 2 3 3 0
50 1 2 4 6 6 4 2 1 3 5 5 3 1 2 4 4 2 1 3 3 1 2 2 1 1 1 2 4 6 6 4 2 1 3 5 5 3 1 2 4 4 2 1 3 3 1 2 2 1 1
0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 4 4 4 5 5 6 7 3 3 3 4 4 4 4 3 3 4 4 4 4 4 5 5 5 5 6 6 6 7 7 8
Formally, for a sequence $$$a$$$ of length $$$n$$$, let's define the folding sequence as a sequence $$$b$$$ of length $$$n$$$ such that:
- $$$b_i$$$ ($$$1\le i\le n$$$) is either $$$1$$$ or $$$-1$$$.
- Let $$$p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j$$$. For all $$$1\le i<j\le n$$$, if $$$p(i)=p(j)$$$, then $$$a_i$$$ should be equal to $$$a_j$$$.
($$$[A]$$$ is the value of boolean expression $$$A$$$. i. e. $$$[A]=1$$$ if $$$A$$$ is true, else $$$[A]=0$$$).
Now we define the number of folds of $$$b$$$ as $$$f(b)=\sum_{i=1}^{n-1}[b_i\ne b_{i+1}]$$$.
The maximum number of folds of $$$a$$$ is $$$F(a)=\max\{ f(b)\mid b \text{ is a folding sequence of }a \}$$$.
| Name |
|---|




