| Central-European Olympiad in Informatics, CEOI 2020, Day 1 (IOI, Unofficial Mirror Contest, Unrated) |
|---|
| Finished |
Everybody knows that Balázs has the fanciest fence in the whole town. It's built up from $$$N$$$ fancy sections. The sections are rectangles standing closely next to each other on the ground. The $$$i$$$th section has integer height $$$h_i$$$ and integer width $$$w_i$$$. We are looking for fancy rectangles on this fancy fence. A rectangle is fancy if:
- its sides are either horizontal or vertical and have integer lengths
- the distance between the rectangle and the ground is integer
- the distance between the rectangle and the left side of the first section is integer
- it's lying completely on sections
The first line contains $$$N$$$ ($$$1\leq N \leq 10^{5}$$$) – the number of sections. The second line contains $$$N$$$ space-separated integers, the $$$i$$$th number is $$$h_i$$$ ($$$1 \leq h_i \leq 10^{9}$$$). The third line contains $$$N$$$ space-separated integers, the $$$i$$$th number is $$$w_i$$$ ($$$1 \leq w_i \leq 10^{9}$$$).
You should print a single integer, the number of fancy rectangles modulo $$$10^9+7$$$. So the output range is $$$0,1,2,\ldots, 10^9+6$$$.
2 1 2 1 2
12
The fence looks like this: 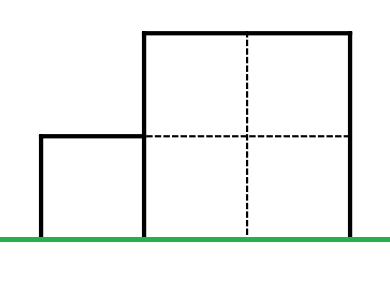
There are 5 fancy rectangles of shape: 
There are 3 fancy rectangles of shape: 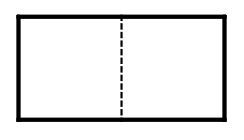
There is 1 fancy rectangle of shape: 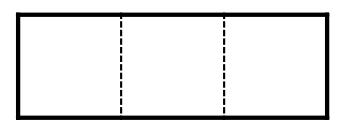
There are 2 fancy rectangles of shape: 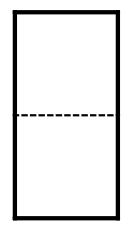
There is 1 fancy rectangle of shape: 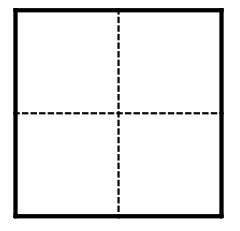
| Name |
|---|




