Gildong живет в городе, в котором система поездов устроена как $$$100$$$ поездов, которые путешествуют от нижнего края до верхнего края и $$$100$$$ поездов, которые путешествуют от левого края до правого края. Поезда на каждой стороне пронумерованы от $$$1$$$ до $$$100$$$ соответственно, и все поезда движутся с одинаковой скоростью. Рассмотрим следующую картинку.
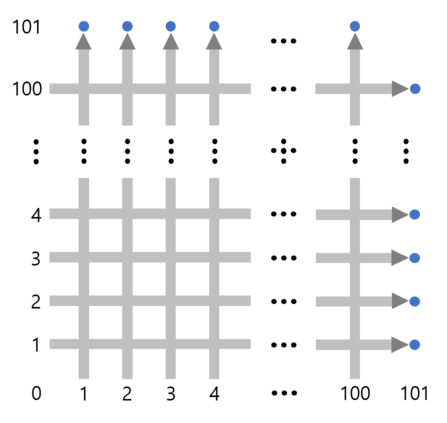
Система поездов может быть описана как координаты на 2D плоскости. $$$i$$$-й поезд, стартующий на нижнем краю, имеет координаты $$$(i,0)$$$ и будет находится в координатах $$$(i,T)$$$ спустя $$$T$$$ минут, а $$$i$$$-й поезд, стартующий на левом краю, имеет координаты $$$(0,i)$$$ и будет находится в координатах $$$(T,i)$$$ спустя $$$T$$$ минут. Все поезда приезжают на место назначения спустя $$$101$$$ минуту.
Gildong обнаружил, что некоторые поезда очень опасно отправлять одновременно. В данный момент $$$n$$$ поездов запланировано отправить с нижнего края, и $$$m$$$ поездов запланировано отправить с левого края. Если два поезда одновременно находятся в одной и той же точке $$$(x,y)$$$ для некоторых $$$x$$$ и $$$y$$$, они врежутся друг в друга. Он попросил вас найти минимальное число поездов, отправку которых нужно отменить, чтобы предотвратить все столкновения.
Каждый тест содержит один или несколько наборов входных данных. В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 100$$$).
Каждый набор входных данных содержит три строки. В первой строке каждого набора входных данных записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 100$$$) — количество поездов, у которых запланирована отправка с нижнего края, и количество поездов, у которых запланирована отправка с левого края, соответственно.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел. Каждое целое число — это номер поезда, у которого запланирована отправка с нижнего края. Числа даны в строго возрастающем порядке и находятся в промежутке от $$$1$$$ до $$$100$$$ включительно.
Третья строка каждого набора входных данных содержит $$$m$$$ целых чисел. Каждое целое число — это номер поезда, у которого запланирована отправка с левого края. Числа даны в строго возрастающем порядке и находятся в промежутке от $$$1$$$ до $$$100$$$ включительно.
Для каждого набора входных данных выведите одно целое число: минимальное количество поездов, отправку которых нужно отменить, чтобы предотвратить все столкновения.
3 1 2 1 3 4 3 2 1 3 4 2 4 9 14 2 7 16 28 33 57 59 86 99 3 9 14 19 25 26 28 35 41 59 85 87 99 100
0 1 3
В первом наборе входных данных можно показать, что текущее расписание не повлечет никаких столкновений. Таким образом, ответ равен нулю.
Во втором наборе входных данных в момент времени $$$T=4$$$ произойдет столкновение, как можно увидеть на картинке ниже. Можно показать, что если отменить отправление одного из этих поездов, то столкновений не произойдет. Таким образом, ответ равен одному.
