| Codeforces Round 699 (Div. 2) |
|---|
| Finished |
Kilani and Abd are neighbors for 3000 years, but then the day came and Kilani decided to move to another house. As a farewell gift, Kilani is going to challenge Abd with a problem written by their other neighbor with the same name Abd.

The problem is:
You are given a connected tree rooted at node $$$1$$$.
You should assign a character a or b to every node in the tree so that the total number of a's is equal to $$$x$$$ and the total number of b's is equal to $$$n - x$$$.
Let's define a string for each node $$$v$$$ of the tree as follows:
- if $$$v$$$ is root then the string is just one character assigned to $$$v$$$:
- otherwise, let's take a string defined for the $$$v$$$'s parent $$$p_v$$$ and add to the end of it a character assigned to $$$v$$$.
You should assign every node a character in a way that minimizes the number of distinct strings among the strings of all nodes.
The first line contains two integers $$$n$$$ and $$$x$$$ ($$$1 \leq n \leq 10^5$$$; $$$0 \leq x \leq n$$$) — the number of vertices in the tree the number of a's.
The second line contains $$$n - 1$$$ integers $$$p_2, p_3, \dots, p_{n}$$$ ($$$1 \leq p_i \leq n$$$; $$$p_i \neq i$$$), where $$$p_i$$$ is the parent of node $$$i$$$.
It is guaranteed that the input describes a connected tree.
In the first line, print the minimum possible total number of distinct strings.
In the second line, print $$$n$$$ characters, where all characters are either a or b and the $$$i$$$-th character is the character assigned to the $$$i$$$-th node.
Make sure that the total number of a's is equal to $$$x$$$ and the total number of b's is equal to $$$n - x$$$.
If there is more than one answer you can print any of them.
9 3 1 2 2 4 4 4 3 1
4 aabbbbbba
The tree from the sample is shown below:
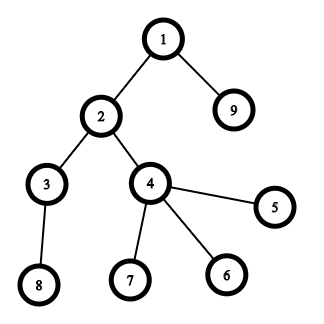
The tree after assigning characters to every node (according to the output) is the following:
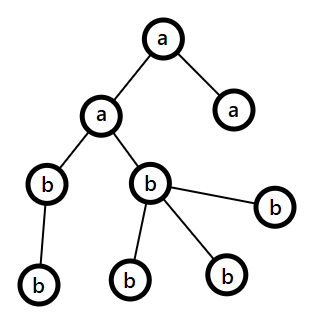
Strings for all nodes are the following:
- string of node $$$1$$$ is: a
- string of node $$$2$$$ is: aa
- string of node $$$3$$$ is: aab
- string of node $$$4$$$ is: aab
- string of node $$$5$$$ is: aabb
- string of node $$$6$$$ is: aabb
- string of node $$$7$$$ is: aabb
- string of node $$$8$$$ is: aabb
- string of node $$$9$$$ is: aa
The set of unique strings is $$$\{\text{a}, \text{aa}, \text{aab}, \text{aabb}\}$$$, so the number of distinct strings is $$$4$$$.
| Name |
|---|




