Berland crossword is a puzzle that is solved on a square grid with $$$n$$$ rows and $$$n$$$ columns. Initially all the cells are white.
To solve the puzzle one has to color some cells on the border of the grid black in such a way that:
- exactly $$$U$$$ cells in the top row are black;
- exactly $$$R$$$ cells in the rightmost column are black;
- exactly $$$D$$$ cells in the bottom row are black;
- exactly $$$L$$$ cells in the leftmost column are black.
Note that you can color zero cells black and leave every cell white.
Your task is to check if there exists a solution to the given puzzle.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 1000$$$) — the number of testcases.
Then the descriptions of $$$t$$$ testcases follow.
The only line of each testcase contains $$$5$$$ integers $$$n, U, R, D, L$$$ ($$$2 \le n \le 100$$$; $$$0 \le U, R, D, L \le n$$$).
For each testcase print "YES" if the solution exists and "NO" otherwise.
You may print every letter in any case you want (so, for example, the strings yEs, yes, Yes and YES are all recognized as positive answer).
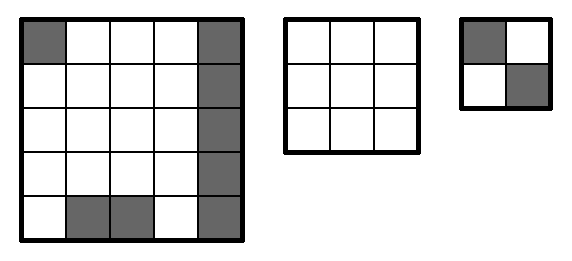
4 5 2 5 3 1 3 0 0 0 0 4 4 1 4 0 2 1 1 1 1
YES YES NO YES
Here are possible solutions to testcases $$$1$$$, $$$2$$$ and $$$4$$$:
| Name |
|---|




