| Codeforces Round 107 (Div. 1) |
|---|
| Finished |
I guess there's not much point in reminding you that Nvodsk winters aren't exactly hot. That increased the popularity of the public transport dramatically. The route of bus 62 has exactly n stops (stop 1 goes first on its way and stop n goes last). The stops are positioned on a straight line and their coordinates are 0 = x1 < x2 < ... < xn.
Each day exactly m people use bus 62. For each person we know the number of the stop where he gets on the bus and the number of the stop where he gets off the bus. A ticket from stop a to stop b (a < b) costs xb - xa rubles. However, the conductor can choose no more than one segment NOT TO SELL a ticket for. We mean that conductor should choose C and D (С <= D) and sell a ticket for the segments [A, C] and [D, B], or not sell the ticket at all. The conductor and the passenger divide the saved money between themselves equally. The conductor's "untaxed income" is sometimes interrupted by inspections that take place as the bus drives on some segment of the route located between two consecutive stops. The inspector fines the conductor by c rubles for each passenger who doesn't have the ticket for this route's segment.
You know the coordinated of all stops xi; the numbers of stops where the i-th passenger gets on and off, ai and bi (ai < bi); the fine c; and also pi — the probability of inspection on segment between the i-th and the i + 1-th stop. The conductor asked you to help him make a plan of selling tickets that maximizes the mathematical expectation of his profit.
The first line contains three integers n, m and c (2 ≤ n ≤ 150 000, 1 ≤ m ≤ 300 000, 1 ≤ c ≤ 10 000).
The next line contains n integers xi (0 ≤ xi ≤ 109, x1 = 0, xi < xi + 1) — the coordinates of the stops on the bus's route.
The third line contains n - 1 integer pi (0 ≤ pi ≤ 100) — the probability of inspection in percents on the segment between stop i and stop i + 1.
Then follow m lines that describe the bus's passengers. Each line contains exactly two integers ai and bi (1 ≤ ai < bi ≤ n) — the numbers of stops where the i-th passenger gets on and off.
Print the single real number — the maximum expectation of the conductor's profit. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 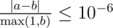 .
.
3 3 10
0 10 100
100 0
1 2
2 3
1 3
90.000000000
10 8 187
0 10 30 70 150 310 630 1270 2550 51100
13 87 65 0 100 44 67 3 4
1 10
2 9
3 8
1 5
6 10
2 7
4 10
4 5
76859.990000000
A comment to the first sample:
The first and third passengers get tickets from stop 1 to stop 2. The second passenger doesn't get a ticket. There always is inspection on the segment 1-2 but both passengers have the ticket for it. There never is an inspection on the segment 2-3, that's why the second passenger gets away with the cheating. Our total profit is (0 + 90 / 2 + 90 / 2) = 90.
| Name |
|---|




