| Codeforces Round 720 (Div. 2) |
|---|
| Finished |
Nastia has an unweighted tree with $$$n$$$ vertices and wants to play with it!
The girl will perform the following operation with her tree, as long as she needs:
- Remove any existing edge.
- Add an edge between any pair of vertices.
What is the minimum number of operations Nastia needs to get a bamboo from a tree? A bamboo is a tree in which no node has a degree greater than $$$2$$$.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10\,000$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of vertices in the tree.
Next $$$n - 1$$$ lines of each test cases describe the edges of the tree in form $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$, $$$a_i \neq b_i$$$).
It's guaranteed the given graph is a tree and the sum of $$$n$$$ in one test doesn't exceed $$$2 \cdot 10^5$$$.
For each test case in the first line print a single integer $$$k$$$ — the minimum number of operations required to obtain a bamboo from the initial tree.
In the next $$$k$$$ lines print $$$4$$$ integers $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ ($$$1 \le x_1, y_1, x_2, y_{2} \le n$$$, $$$x_1 \neq y_1$$$, $$$x_2 \neq y_2$$$) — this way you remove the edge $$$(x_1, y_1)$$$ and add an undirected edge $$$(x_2, y_2)$$$.
Note that the edge $$$(x_1, y_1)$$$ must be present in the graph at the moment of removing.
2 7 1 2 1 3 2 4 2 5 3 6 3 7 4 1 2 1 3 3 4
2 2 5 6 7 3 6 4 5 0
Note the graph can be unconnected after a certain operation.
Consider the first test case of the example:
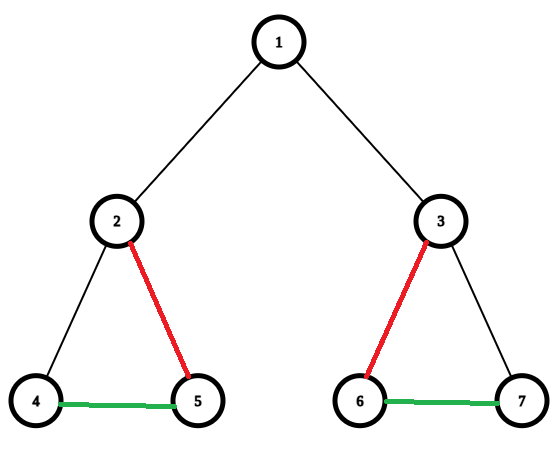
| Name |
|---|




