| Codeforces Round 722 (Div. 1) |
|---|
| Finished |
Parsa has a humongous tree on $$$n$$$ vertices.
On each vertex $$$v$$$ he has written two integers $$$l_v$$$ and $$$r_v$$$.
To make Parsa's tree look even more majestic, Nima wants to assign a number $$$a_v$$$ ($$$l_v \le a_v \le r_v$$$) to each vertex $$$v$$$ such that the beauty of Parsa's tree is maximized.
Nima's sense of the beauty is rather bizarre. He defines the beauty of the tree as the sum of $$$|a_u - a_v|$$$ over all edges $$$(u, v)$$$ of the tree.
Since Parsa's tree is too large, Nima can't maximize its beauty on his own. Your task is to find the maximum possible beauty for Parsa's tree.
The first line contains an integer $$$t$$$ $$$(1\le t\le 250)$$$ — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ $$$(2\le n\le 10^5)$$$ — the number of vertices in Parsa's tree.
The $$$i$$$-th of the following $$$n$$$ lines contains two integers $$$l_i$$$ and $$$r_i$$$ $$$(1 \le l_i \le r_i \le 10^9)$$$.
Each of the next $$$n-1$$$ lines contains two integers $$$u$$$ and $$$v$$$ $$$(1 \le u , v \le n, u\neq v)$$$ meaning that there is an edge between the vertices $$$u$$$ and $$$v$$$ in Parsa's tree.
It is guaranteed that the given graph is a tree.
It is guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^5$$$.
For each test case print the maximum possible beauty for Parsa's tree.
3 2 1 6 3 8 1 2 3 1 3 4 6 7 9 1 2 2 3 6 3 14 12 20 12 19 2 12 10 17 3 17 3 2 6 5 1 5 2 6 4 6
7 8 62
The trees in the example:
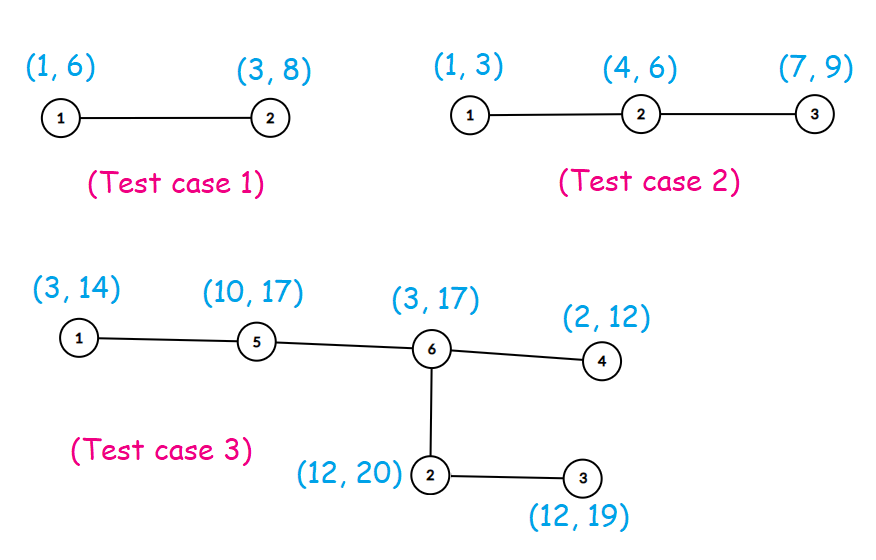
In the first test case, one possible assignment is $$$a = \{1, 8\}$$$ which results in $$$|1 - 8| = 7$$$.
In the second test case, one of the possible assignments is $$$a = \{1, 5, 9\}$$$ which results in a beauty of $$$|1 - 5| + |5 - 9| = 8$$$
| Name |
|---|




