$$$2^k$$$ teams participate in a playoff tournament. The tournament consists of $$$2^k - 1$$$ games. They are held as follows: first of all, the teams are split into pairs: team $$$1$$$ plays against team $$$2$$$, team $$$3$$$ plays against team $$$4$$$ (exactly in this order), and so on (so, $$$2^{k-1}$$$ games are played in that phase). When a team loses a game, it is eliminated, and each game results in elimination of one team (there are no ties). After that, only $$$2^{k-1}$$$ teams remain. If only one team remains, it is declared the champion; otherwise, $$$2^{k-2}$$$ games are played: in the first one of them, the winner of the game "$$$1$$$ vs $$$2$$$" plays against the winner of the game "$$$3$$$ vs $$$4$$$", then the winner of the game "$$$5$$$ vs $$$6$$$" plays against the winner of the game "$$$7$$$ vs $$$8$$$", and so on. This process repeats until only one team remains.
For example, this picture describes the chronological order of games with $$$k = 3$$$:
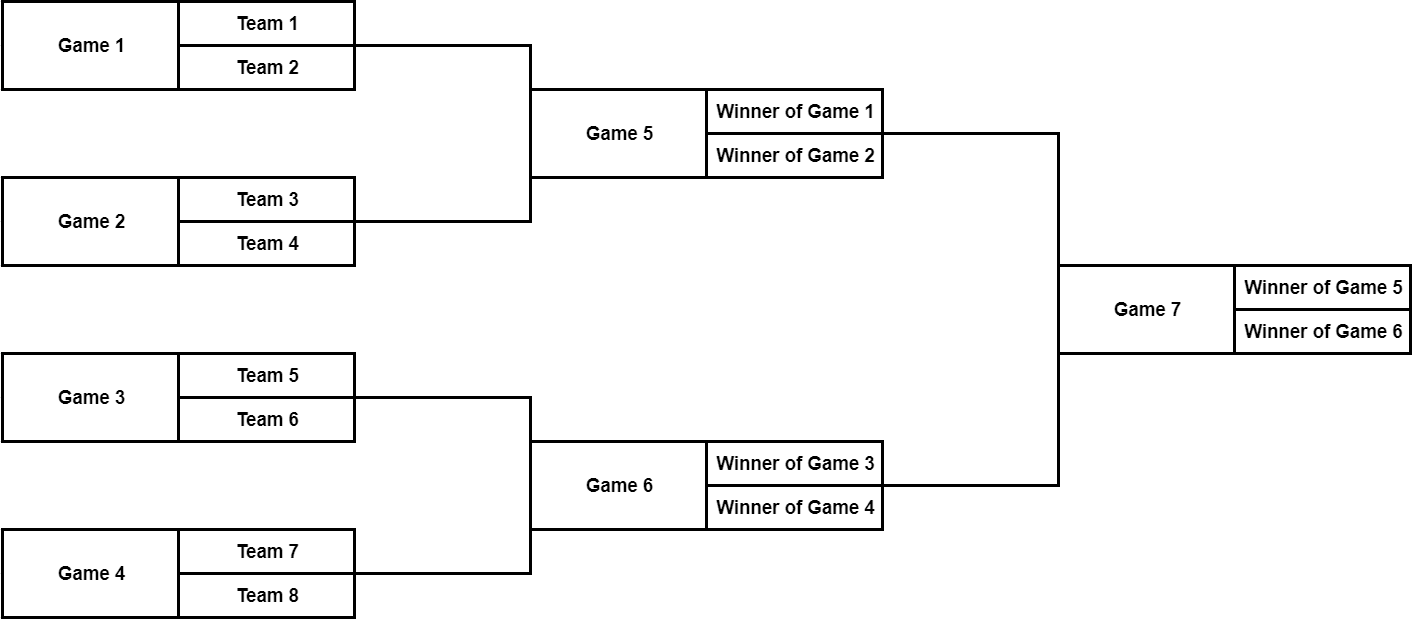
Let the string $$$s$$$ consisting of $$$2^k - 1$$$ characters describe the results of the games in chronological order as follows:
- if $$$s_i$$$ is 0, then the team with lower index wins the $$$i$$$-th game;
- if $$$s_i$$$ is 1, then the team with greater index wins the $$$i$$$-th game;
- if $$$s_i$$$ is ?, then the result of the $$$i$$$-th game is unknown (any team could win this game).
Let $$$f(s)$$$ be the number of possible winners of the tournament described by the string $$$s$$$. A team $$$i$$$ is a possible winner of the tournament if it is possible to replace every ? with either 1 or 0 in such a way that team $$$i$$$ is the champion.
You are given the initial state of the string $$$s$$$. You have to process $$$q$$$ queries of the following form:
- $$$p$$$ $$$c$$$ — replace $$$s_p$$$ with character $$$c$$$, and print $$$f(s)$$$ as the result of the query.
The first line contains one integer $$$k$$$ ($$$1 \le k \le 18$$$).
The second line contains a string consisting of $$$2^k - 1$$$ characters — the initial state of the string $$$s$$$. Each character is either ?, 0, or 1.
The third line contains one integer $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — the number of queries.
Then $$$q$$$ lines follow, the $$$i$$$-th line contains an integer $$$p$$$ and a character $$$c$$$ ($$$1 \le p \le 2^k - 1$$$; $$$c$$$ is either ?, 0, or 1), describing the $$$i$$$-th query.
For each query, print one integer — $$$f(s)$$$.
3 0110?11 6 5 1 6 ? 7 ? 1 ? 5 ? 1 1
1 2 3 3 5 4
| Name |
|---|




