| Codeforces Round 731 (Div. 3) |
|---|
| Finished |
On a strip of land of length $$$n$$$ there are $$$k$$$ air conditioners: the $$$i$$$-th air conditioner is placed in cell $$$a_i$$$ ($$$1 \le a_i \le n$$$). Two or more air conditioners cannot be placed in the same cell (i.e. all $$$a_i$$$ are distinct).
Each air conditioner is characterized by one parameter: temperature. The $$$i$$$-th air conditioner is set to the temperature $$$t_i$$$.
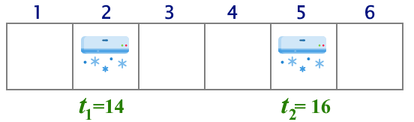 Example of strip of length $$$n=6$$$, where $$$k=2$$$, $$$a=[2,5]$$$ and $$$t=[14,16]$$$.
Example of strip of length $$$n=6$$$, where $$$k=2$$$, $$$a=[2,5]$$$ and $$$t=[14,16]$$$. For each cell $$$i$$$ ($$$1 \le i \le n$$$) find it's temperature, that can be calculated by the formula $$$$$$\min_{1 \le j \le k}(t_j + |a_j - i|),$$$$$$
where $$$|a_j - i|$$$ denotes absolute value of the difference $$$a_j - i$$$.
In other words, the temperature in cell $$$i$$$ is equal to the minimum among the temperatures of air conditioners, increased by the distance from it to the cell $$$i$$$.
Let's look at an example. Consider that $$$n=6, k=2$$$, the first air conditioner is placed in cell $$$a_1=2$$$ and is set to the temperature $$$t_1=14$$$ and the second air conditioner is placed in cell $$$a_2=5$$$ and is set to the temperature $$$t_2=16$$$. In that case temperatures in cells are:
- temperature in cell $$$1$$$ is: $$$\min(14 + |2 - 1|, 16 + |5 - 1|)=\min(14 + 1, 16 + 4)=\min(15, 20)=15$$$;
- temperature in cell $$$2$$$ is: $$$\min(14 + |2 - 2|, 16 + |5 - 2|)=\min(14 + 0, 16 + 3)=\min(14, 19)=14$$$;
- temperature in cell $$$3$$$ is: $$$\min(14 + |2 - 3|, 16 + |5 - 3|)=\min(14 + 1, 16 + 2)=\min(15, 18)=15$$$;
- temperature in cell $$$4$$$ is: $$$\min(14 + |2 - 4|, 16 + |5 - 4|)=\min(14 + 2, 16 + 1)=\min(16, 17)=16$$$;
- temperature in cell $$$5$$$ is: $$$\min(14 + |2 - 5|, 16 + |5 - 5|)=\min(14 + 3, 16 + 0)=\min(17, 16)=16$$$;
- temperature in cell $$$6$$$ is: $$$\min(14 + |2 - 6|, 16 + |5 - 6|)=\min(14 + 4, 16 + 1)=\min(18, 17)=17$$$.
For each cell from $$$1$$$ to $$$n$$$ find the temperature in it.
The first line contains one integer $$$q$$$ ($$$1 \le q \le 10^4$$$) — the number of test cases in the input. Then test cases follow. Before each test case, there is an empty line.
Each test case contains three lines. The first line contains two integers $$$n$$$ ($$$1 \le n \le 3 \cdot 10^5$$$) and $$$k$$$ ($$$1 \le k \le n$$$) — the length of the strip of land and the number of air conditioners respectively.
The second line contains $$$k$$$ integers $$$a_1, a_2, \ldots, a_k$$$ ($$$1 \le a_i \le n$$$) — positions of air conditioners on the strip of land.
The third line contains $$$k$$$ integers $$$t_1, t_2, \ldots, t_k$$$ ($$$1 \le t_i \le 10^9$$$) — temperatures of air conditioners.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$3 \cdot 10^5$$$.
For each test case output $$$n$$$ integers separated by space: temperatures of air in cells.
5 6 2 2 5 14 16 10 1 7 30 5 5 3 1 4 2 5 3 1 4 2 5 7 1 1 1000000000 6 3 6 1 3 5 5 5
15 14 15 16 16 17 36 35 34 33 32 31 30 31 32 33 1 2 3 4 5 1000000000 1000000001 1000000002 1000000003 1000000004 1000000005 1000000006 5 6 5 6 6 5
| Name |
|---|




