
As mentioned previously William really likes playing video games. In one of his favorite games, the player character is in a universe where every planet is designated by a binary number from $$$0$$$ to $$$2^n - 1$$$. On each planet, there are gates that allow the player to move from planet $$$i$$$ to planet $$$j$$$ if the binary representations of $$$i$$$ and $$$j$$$ differ in exactly one bit.
William wants to test you and see how you can handle processing the following queries in this game universe:
- Destroy planets with numbers from $$$l$$$ to $$$r$$$ inclusively. These planets cannot be moved to anymore.
- Figure out if it is possible to reach planet $$$b$$$ from planet $$$a$$$ using some number of planetary gates. It is guaranteed that the planets $$$a$$$ and $$$b$$$ are not destroyed.
The first line contains two integers $$$n$$$, $$$m$$$ ($$$1 \leq n \leq 50$$$, $$$1 \leq m \leq 5 \cdot 10^4$$$), which are the number of bits in binary representation of each planets' designation and the number of queries, respectively.
Each of the next $$$m$$$ lines contains a query of two types:
block l r — query for destruction of planets with numbers from $$$l$$$ to $$$r$$$ inclusively ($$$0 \le l \le r < 2^n$$$). It's guaranteed that no planet will be destroyed twice.
ask a b — query for reachability between planets $$$a$$$ and $$$b$$$ ($$$0 \le a, b < 2^n$$$). It's guaranteed that planets $$$a$$$ and $$$b$$$ hasn't been destroyed yet.
For each query of type ask you must output "1" in a new line, if it is possible to reach planet $$$b$$$ from planet $$$a$$$ and "0" otherwise (without quotation marks).
3 3 ask 0 7 block 3 6 ask 0 7
1 0
6 10 block 12 26 ask 44 63 block 32 46 ask 1 54 block 27 30 ask 10 31 ask 11 31 ask 49 31 block 31 31 ask 2 51
1 1 0 0 1 0
The first example test can be visualized in the following way:
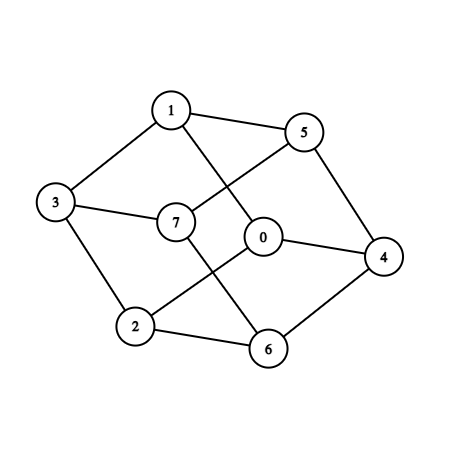
Response to a query ask 0 7 is positive.
Next after query block 3 6 the graph will look the following way (destroyed vertices are highlighted):
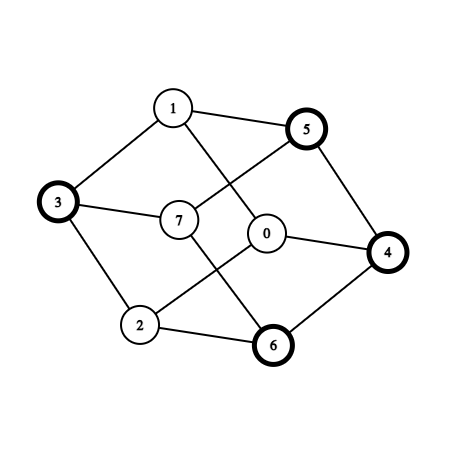
Response to a query ask 0 7 is negative, since any path from vertex $$$0$$$ to vertex $$$7$$$ must go through one of the destroyed vertices.
| Name |
|---|




