This is an interactive problem.
Your goal is to find a circle on a plane by shooting rays and getting the distance to the circle as a result.
Interactor has three hidden integer parameters that are determined in advance for each test, but which you don't know — $$$x_c$$$, $$$y_c$$$, and $$$r_c$$$. $$$(x_c, y_c)$$$ are coordinates of the circle's center and $$$r_c$$$ is its radius. The absolute values of $$$x_c$$$, $$$y_c$$$, and $$$r_c$$$ do not exceed $$$10^5$$$, and $$$1 \leq r_c \leq \sqrt{x_c^2 + y_c^2} - 1$$$.
You can shoot rays that extend from the origin $$$(0,0)$$$ and go via a point $$$(x_q,y_q)$$$ with the integer coordinates you specify. For each ray, you get a distance from the ray to the circle or $$$0$$$ if the ray intersects the circle.
The interaction starts with your program printing a query to the standard output and finishes when your program finds and prints the answer to the problem.
Each query has a form of "? $$$x_q$$$ $$$y_q$$$", where $$$x_q$$$ and $$$y_q$$$ are integers ($$$|x_q|, |y_q| \le 10^6$$$; $$$x_q \ne 0$$$ or $$$y_q \ne 0$$$).
The interactor outputs a line with a single floating-point number — the distance between a query ray and a circle that is precise to $$$10^{-10}$$$ by an absolute value.
Your program can make the next query, read the output, and so on. You are allowed to do at most $$$60$$$ queries. At the end of the interaction, print the answer line "! $$$x_c$$$ $$$y_c$$$ $$$r_c$$$", flush the output and exit.
Note, that the output of the interactor is actually rounded to the 10-th digit after a decimal point, so if you are stress-testing your solution locally, make sure that you also perform the corresponding rounding.
? 0 -10 ? 10 -10 ? 10 0 ? 10 10 ? 10 20 ? 10 30 ! 20 10 10
12.360679775 11.2132034356 0.0 0.0 3.416407865 5.8113883008
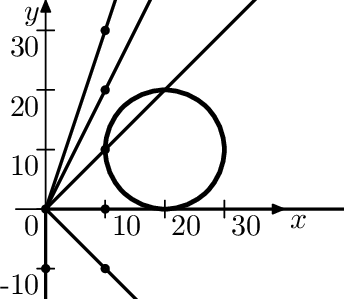 Illustration of the queries from the example interaction.
Illustration of the queries from the example interaction.
| Name |
|---|




