| Codeforces Round 111 (Div. 2) |
|---|
| Finished |
You are given a connected weighted undirected graph without any loops and multiple edges.
Let us remind you that a graph's spanning tree is defined as an acyclic connected subgraph of the given graph that includes all of the graph's vertexes. The weight of a tree is defined as the sum of weights of the edges that the given tree contains. The minimum spanning tree (MST) of a graph is defined as the graph's spanning tree having the minimum possible weight. For any connected graph obviously exists the minimum spanning tree, but in the general case, a graph's minimum spanning tree is not unique.
Your task is to determine the following for each edge of the given graph: whether it is either included in any MST, or included at least in one MST, or not included in any MST.
The first line contains two integers n and m (2 ≤ n ≤ 105, 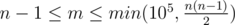 ) — the number of the graph's vertexes and edges, correspondingly. Then follow m lines, each of them contains three integers — the description of the graph's edges as "ai bi wi" (1 ≤ ai, bi ≤ n, 1 ≤ wi ≤ 106, ai ≠ bi), where ai and bi are the numbers of vertexes connected by the i-th edge, wi is the edge's weight. It is guaranteed that the graph is connected and doesn't contain loops or multiple edges.
) — the number of the graph's vertexes and edges, correspondingly. Then follow m lines, each of them contains three integers — the description of the graph's edges as "ai bi wi" (1 ≤ ai, bi ≤ n, 1 ≤ wi ≤ 106, ai ≠ bi), where ai and bi are the numbers of vertexes connected by the i-th edge, wi is the edge's weight. It is guaranteed that the graph is connected and doesn't contain loops or multiple edges.
Print m lines — the answers for all edges. If the i-th edge is included in any MST, print "any"; if the i-th edge is included at least in one MST, print "at least one"; if the i-th edge isn't included in any MST, print "none". Print the answers for the edges in the order in which the edges are specified in the input.
4 5
1 2 101
1 3 100
2 3 2
2 4 2
3 4 1
none
any
at least one
at least one
any
3 3
1 2 1
2 3 1
1 3 2
any
any
none
3 3
1 2 1
2 3 1
1 3 1
at least one
at least one
at least one
In the second sample the MST is unique for the given graph: it contains two first edges.
In the third sample any two edges form the MST for the given graph. That means that each edge is included at least in one MST.
| Name |
|---|




