| Codeforces Round 783 (Div. 1) |
|---|
| Finished |
You are given a board with $$$n$$$ rows and $$$n$$$ columns, numbered from $$$1$$$ to $$$n$$$. The intersection of the $$$a$$$-th row and $$$b$$$-th column is denoted by $$$(a, b)$$$.
A half-queen attacks cells in the same row, same column, and on one diagonal. More formally, a half-queen on $$$(a, b)$$$ attacks the cell $$$(c, d)$$$ if $$$a=c$$$ or $$$b=d$$$ or $$$a-b=c-d$$$.
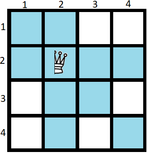 The blue cells are under attack.
The blue cells are under attack. Construct an optimal solution.
The first line contains a single integer $$$n$$$ ($$$1 \le n \le 10^5$$$) — the size of the board.
In the first line print a single integer $$$k$$$ — the minimum number of half-queens.
In each of the next $$$k$$$ lines print two integers $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$) — the position of the $$$i$$$-th half-queen.
If there are multiple solutions, print any.
1
1 1 1
2
1 1 1
3
2 1 1 1 2
Example $$$1$$$: one half-queen is enough. Note: a half-queen on $$$(1, 1)$$$ attacks $$$(1, 1)$$$.
Example $$$2$$$: one half-queen is enough too. $$$(1, 2)$$$ or $$$(2, 1)$$$ would be wrong solutions, because a half-queen on $$$(1, 2)$$$ does not attack the cell $$$(2, 1)$$$ and vice versa. $$$(2, 2)$$$ is also a valid solution.
Example $$$3$$$: it is impossible to cover the board with one half queen. There are multiple solutions for $$$2$$$ half-queens; you can print any of them.
| Name |
|---|




