| Codeforces Round 786 (Div. 3) |
|---|
| Finished |
You are given a directed acyclic graph, consisting of $$$n$$$ vertices and $$$m$$$ edges. The vertices are numbered from $$$1$$$ to $$$n$$$. There are no multiple edges and self-loops.
Let $$$\mathit{in}_v$$$ be the number of incoming edges (indegree) and $$$\mathit{out}_v$$$ be the number of outgoing edges (outdegree) of vertex $$$v$$$.
You are asked to remove some edges from the graph. Let the new degrees be $$$\mathit{in'}_v$$$ and $$$\mathit{out'}_v$$$.
You are only allowed to remove the edges if the following conditions hold for every vertex $$$v$$$:
- $$$\mathit{in'}_v < \mathit{in}_v$$$ or $$$\mathit{in'}_v = \mathit{in}_v = 0$$$;
- $$$\mathit{out'}_v < \mathit{out}_v$$$ or $$$\mathit{out'}_v = \mathit{out}_v = 0$$$.
Let's call a set of vertices $$$S$$$ cute if for each pair of vertices $$$v$$$ and $$$u$$$ ($$$v \neq u$$$) such that $$$v \in S$$$ and $$$u \in S$$$, there exists a path either from $$$v$$$ to $$$u$$$ or from $$$u$$$ to $$$v$$$ over the non-removed edges.
What is the maximum possible size of a cute set $$$S$$$ after you remove some edges from the graph and both indegrees and outdegrees of all vertices either decrease or remain equal to $$$0$$$?
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$; $$$0 \le m \le 2 \cdot 10^5$$$) — the number of vertices and the number of edges of the graph.
Each of the next $$$m$$$ lines contains two integers $$$v$$$ and $$$u$$$ ($$$1 \le v, u \le n$$$; $$$v \neq u$$$) — the description of an edge.
The given edges form a valid directed acyclic graph. There are no multiple edges.
Print a single integer — the maximum possible size of a cute set $$$S$$$ after you remove some edges from the graph and both indegrees and outdegrees of all vertices either decrease or remain equal to $$$0$$$.
3 3 1 2 2 3 1 3
2
5 0
1
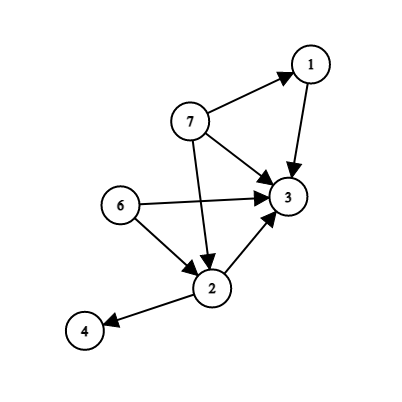
7 8 7 1 1 3 6 2 2 3 7 2 2 4 7 3 6 3
3
In the first example, you can remove edges $$$(1, 2)$$$ and $$$(2, 3)$$$. $$$\mathit{in} = [0, 1, 2]$$$, $$$\mathit{out} = [2, 1, 0]$$$. $$$\mathit{in'} = [0, 0, 1]$$$, $$$\mathit{out'} = [1, 0, 0]$$$. You can see that for all $$$v$$$ the conditions hold. The maximum cute set $$$S$$$ is formed by vertices $$$1$$$ and $$$3$$$. They are still connected directly by an edge, so there is a path between them.
In the second example, there are no edges. Since all $$$\mathit{in}_v$$$ and $$$\mathit{out}_v$$$ are equal to $$$0$$$, leaving a graph with zero edges is allowed. There are $$$5$$$ cute sets, each contains a single vertex. Thus, the maximum size is $$$1$$$.
In the third example, you can remove edges $$$(7, 1)$$$, $$$(2, 4)$$$, $$$(1, 3)$$$ and $$$(6, 2)$$$. The maximum cute set will be $$$S = \{7, 3, 2\}$$$. You can remove edge $$$(7, 3)$$$ as well, and the answer won't change.
Here is the picture of the graph from the third example:
| Name |
|---|




