You are given a grid with $$$n$$$ rows and $$$m$$$ columns. We denote the square on the $$$i$$$-th ($$$1\le i\le n$$$) row and $$$j$$$-th ($$$1\le j\le m$$$) column by $$$(i, j)$$$ and the number there by $$$a_{ij}$$$. All numbers are equal to $$$1$$$ or to $$$-1$$$.
You start from the square $$$(1, 1)$$$ and can move one square down or one square to the right at a time. In the end, you want to end up at the square $$$(n, m)$$$.
Is it possible to move in such a way so that the sum of the values written in all the visited cells (including $$$a_{11}$$$ and $$$a_{nm}$$$) is $$$0$$$?
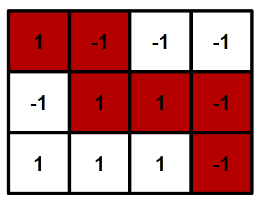
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \leq t \leq 10^4$$$). Description of the test cases follows.
The first line of each test case contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 1000$$$) — the size of the grid.
Each of the following $$$n$$$ lines contains $$$m$$$ integers. The $$$j$$$-th integer on the $$$i$$$-th line is $$$a_{ij}$$$ ($$$a_{ij} = 1$$$ or $$$-1$$$) — the element in the cell $$$(i, j)$$$.
It is guaranteed that the sum of $$$n\cdot m$$$ over all test cases does not exceed $$$10^6$$$.
For each test case, print "YES" if there exists a path from the top left to the bottom right that adds up to $$$0$$$, and "NO" otherwise. You can output each letter in any case.
51 111 21 -11 41 -1 1 -13 41 -1 -1 -1-1 1 1 -11 1 1 -13 41 -1 1 1-1 1 -1 11 -1 1 1
NO YES YES YES NO
One possible path for the fourth test case is given in the picture in the statement.
| Name |
|---|




