| Codeforces Global Round 21 |
|---|
| Finished |
A permutation is an array consisting of $$$n$$$ distinct integers from $$$1$$$ to $$$n$$$ in arbitrary order. For example, $$$[2,3,1,5,4]$$$ is a permutation, but $$$[1,2,2]$$$ is not a permutation ($$$2$$$ appears twice in the array) and $$$[1,3,4]$$$ is also not a permutation ($$$n=3$$$ but there is $$$4$$$ in the array).
You are given a permutation of $$$1,2,\dots,n$$$, $$$[a_1,a_2,\dots,a_n]$$$. For integers $$$i$$$, $$$j$$$ such that $$$1\le i<j\le n$$$, define $$$\operatorname{mn}(i,j)$$$ as $$$\min\limits_{k=i}^j a_k$$$, and define $$$\operatorname{mx}(i,j)$$$ as $$$\max\limits_{k=i}^j a_k$$$.
Let us build an undirected graph of $$$n$$$ vertices, numbered $$$1$$$ to $$$n$$$. For every pair of integers $$$1\le i<j\le n$$$, if $$$\operatorname{mn}(i,j)=a_i$$$ and $$$\operatorname{mx}(i,j)=a_j$$$ both holds, or $$$\operatorname{mn}(i,j)=a_j$$$ and $$$\operatorname{mx}(i,j)=a_i$$$ both holds, add an undirected edge of length $$$1$$$ between vertices $$$i$$$ and $$$j$$$.
In this graph, find the length of the shortest path from vertex $$$1$$$ to vertex $$$n$$$. We can prove that $$$1$$$ and $$$n$$$ will always be connected via some path, so a shortest path always exists.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 5\cdot 10^4$$$). Description of the test cases follows.
The first line of each test case contains one integer $$$n$$$ ($$$1\le n\le 2.5\cdot 10^5$$$).
The second line of each test case contains $$$n$$$ integers $$$a_1$$$, $$$a_2$$$, $$$\ldots$$$, $$$a_n$$$ ($$$1\le a_i\le n$$$). It's guaranteed that $$$a$$$ is a permutation of $$$1$$$, $$$2$$$, $$$\dots$$$, $$$n$$$.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$5\cdot 10^5$$$.
For each test case, print a single line containing one integer — the length of the shortest path from $$$1$$$ to $$$n$$$.
51121 251 4 2 3 552 1 5 3 4107 4 8 1 6 10 3 5 2 9
0 1 1 4 6
The following are illustrations of constructed graphs in example test cases.
 the constructed graph in test case 1
the constructed graph in test case 1 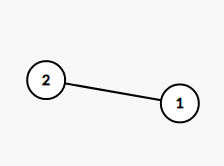 the constructed graph in test case 2
the constructed graph in test case 2 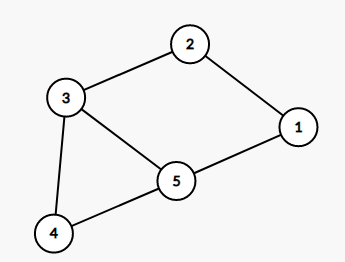 the constructed graph in test case 3
the constructed graph in test case 3 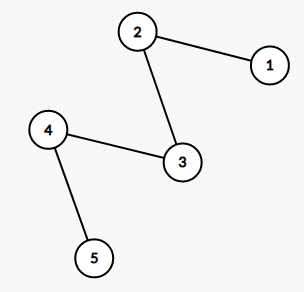 the constructed graph in test case 4
the constructed graph in test case 4 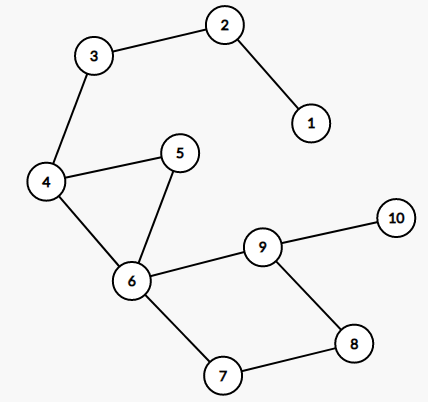 the constructed graph in test case 5
the constructed graph in test case 5
| Name |
|---|




