| Codeforces Round 802 (Div. 2) |
|---|
| Finished |
You are given a table $$$a$$$ of size $$$n \times m$$$. We will consider the table rows numbered from top to bottom from $$$1$$$ to $$$n$$$, and the columns numbered from left to right from $$$1$$$ to $$$m$$$. We will denote a cell that is in the $$$i$$$-th row and in the $$$j$$$-th column as $$$(i, j)$$$. In the cell $$$(i, j)$$$ there is written a number $$$(i - 1) \cdot m + j$$$, that is $$$a_{ij} = (i - 1) \cdot m + j$$$.
A turtle initially stands in the cell $$$(1, 1)$$$ and it wants to come to the cell $$$(n, m)$$$. From the cell $$$(i, j)$$$ it can in one step go to one of the cells $$$(i + 1, j)$$$ or $$$(i, j + 1)$$$, if it exists. A path is a sequence of cells in which for every two adjacent in the sequence cells the following satisfies: the turtle can reach from the first cell to the second cell in one step. A cost of a path is the sum of numbers that are written in the cells of the path.
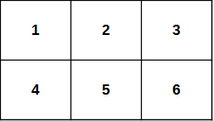
For example, with $$$n = 2$$$ and $$$m = 3$$$ the table will look as shown above. The turtle can take the following path: $$$(1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3)$$$. The cost of such way is equal to $$$a_{11} + a_{12} + a_{13} + a_{23} = 12$$$. On the other hand, the paths $$$(1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1)$$$ and $$$(1, 1) \rightarrow (1, 3)$$$ are incorrect, because in the first path the turtle can't make a step $$$(2, 2) \rightarrow (2, 1)$$$, and in the second path it can't make a step $$$(1, 1) \rightarrow (1, 3)$$$.
You are asked to tell the turtle a minimal possible cost of a path from the cell $$$(1, 1)$$$ to the cell $$$(n, m)$$$. Please note that the cells $$$(1, 1)$$$ and $$$(n, m)$$$ are a part of the way.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases. The description of test cases follows.
A single line of each test case contains two integers $$$n$$$ and $$$m$$$ ($$$1 \leq n, m \leq 10^4$$$) — the number of rows and columns of the table $$$a$$$ respectively.
For each test case output a single integer — a minimal possible cost of a path from the cell $$$(1, 1)$$$ to the cell $$$(n, m)$$$.
71 12 33 27 11 105 510000 10000
1 12 13 28 55 85 500099995000
In the first test case the only possible path consists of a single cell $$$(1, 1)$$$.
The path with the minimal cost in the second test case is shown in the statement.
In the fourth and the fifth test cases there is only one path from $$$(1, 1)$$$ to $$$(n, m)$$$. Both paths visit every cell in the table.
| Name |
|---|




