| Codeforces Round 812 (Div. 2) |
|---|
| Finished |
You are given a square matrix $$$A$$$ of size $$$n \times n$$$ whose elements are integers. We will denote the element on the intersection of the $$$i$$$-th row and the $$$j$$$-th column as $$$A_{i,j}$$$.
You can perform operations on the matrix. In each operation, you can choose an integer $$$k$$$, then for each index $$$i$$$ ($$$1 \leq i \leq n$$$), swap $$$A_{i, k}$$$ with $$$A_{k, i}$$$. Note that cell $$$A_{k, k}$$$ remains unchanged.
For example, for $$$n = 4$$$ and $$$k = 3$$$, this matrix will be transformed like this:
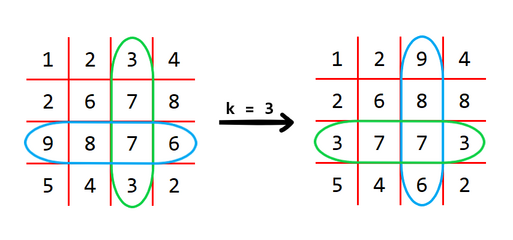 The operation $$$k = 3$$$ swaps the blue row with the green column.
The operation $$$k = 3$$$ swaps the blue row with the green column. You can perform this operation any number of times. Find the lexicographically smallest matrix$$$^\dagger$$$ you can obtain after performing arbitrary number of operations.
$$${}^\dagger$$$ For two matrices $$$A$$$ and $$$B$$$ of size $$$n \times n$$$, let $$$a_{(i-1) \cdot n + j} = A_{i,j}$$$ and $$$b_{(i-1) \cdot n + j} = B_{i,j}$$$. Then, the matrix $$$A$$$ is lexicographically smaller than the matrix $$$B$$$ when there exists an index $$$i$$$ ($$$1 \leq i \leq n^2$$$) such that $$$a_i < b_i$$$ and for all indices $$$j$$$ such that $$$1 \leq j < i$$$, $$$a_j = b_j$$$.
The first line contains a single integer $$$t$$$ ($$$1 \leq t \leq 10^5$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 1000$$$) — the size of the matrix.
The $$$i$$$-th line of the next $$$n$$$ lines contains $$$n$$$ integers $$$A_{i, 1}, A_{i, 2}, \dots, A_{i, n}$$$ ($$$1 \le A_{i, j} \le 10^9$$$) — description of the matrix $$$A$$$.
It is guaranteed that the sum of $$$n^2$$$ over all test cases does not exceed $$$10^6$$$.
For each test case, print $$$n$$$ lines with $$$n$$$ integers each — the lexicographically smallest matrix.
232 1 22 1 21 1 243 3 1 21 1 3 13 2 3 22 3 3 1
2 1 1 2 1 1 2 2 2 3 1 1 2 3 1 2 1 3 3 3 3 2 3 2 1
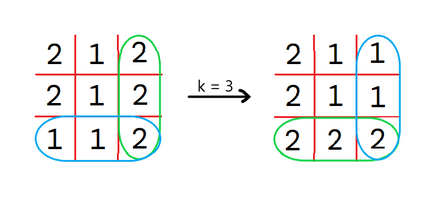
Note that in every picture below the matrix is transformed in such a way that the blue rows are swapped with the green columns.
In the first test case, we can perform $$$1$$$ operation for $$$k = 3$$$. The matrix will be transformed as below:


| Name |
|---|




