| Codeforces Round 824 (Div. 2) |
|---|
| Закончено |
В вашем городке есть $$$n$$$ домов, расположенных на числовой прямой в точках $$$h_1, h_2, \ldots, h_n$$$. Вы хотите построить себе новый дом и рассматриваете два варианта, где его разместить: точки $$$p_1$$$ и $$$p_2$$$.
Так как вы любите ходить в гости, вы заблаговременно вычислили для обеих точек расстояния до уже существующих домов. Более формально, вы вычислили два массива $$$d_1$$$, $$$d_2$$$: $$$d_{i, j} = \left|p_i - h_j\right|$$$, где $$$|x|$$$ обозначает модуль числа $$$x$$$.
Спустя долгое время бездействия вы забыли расположение домов $$$h$$$ и планируемые точки $$$p_1$$$, $$$p_2$$$. Но в вашем дневнике нашлись два массива — $$$d_1$$$, $$$d_2$$$, в подлинности которых вы сомневаетесь. Также значения внутри каждого из массивов могли перемешаться, поэтому значения на одинаковых позициях массивов $$$d_1$$$ и $$$d_2$$$ могут соответствовать разным домам. Обратите внимание, что значения из одного массива не могли попасть в другой, иными словами, все значения в массиве $$$d_1$$$ соответствуют расстоянию от $$$p_1$$$ до домов, а в массиве $$$d_2$$$ — от $$$p_2$$$ до домов.
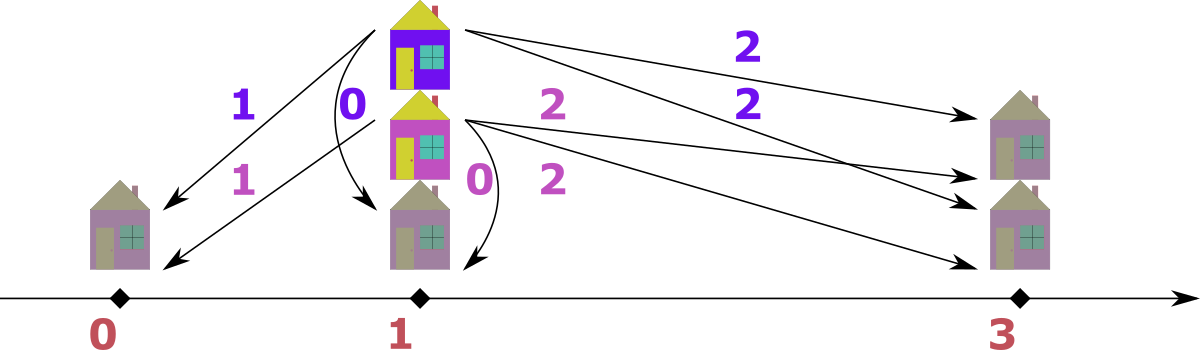
Обратите внимание, что расположения домов $$$h_i$$$ и рассматриваемых вариантов $$$p_j$$$ могли совпадать. Например, корректными являются расположения $$$h = \{1, 0, 3, 3\}$$$, $$$p = \{1, 1\}$$$, которым могли соответствовать уже перемешанные $$$d_1 = \{0, 2, 1, 2\}$$$, $$$d_2 = \{2, 2, 1, 0\}$$$.
Проверьте, существуют ли расположение домов $$$h$$$ и планируемые точки $$$p_1$$$, $$$p_2$$$, для которых бы найденные массивы расстояний были корректными. Если такое возможно, найдите подходящее расположение домов и мест строительства.
Первая строка входных данных содержит единственное целое число $$$t$$$ ($$$1 \le t \le 10^3$$$) — количество наборов входных данных. Описание наборов входных данных следует ниже.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^3$$$) — длину массивов $$$d_1$$$, $$$d_2$$$.
Следующие две строки содержат по $$$n$$$ целых чисел: массивы $$$d_1$$$ и $$$d_2$$$ ($$$0 \le d_{i, j} \le 10^9$$$) соответственно.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^3$$$.
Для каждого набора входных данных выведите одну строку «NO», если ответа не существует.
Иначе выведите три строки. Первая строка должна содержать «YES». Вторая строка должна содержать $$$n$$$ целых чисел $$$h_1, h_2, \ldots, h_n$$$. Третья строка должна содержать два целых числа $$$p_1$$$, $$$p_2$$$.
Должно выполняться $$$0 \le h_i, p_1, p_2 \le 2 \cdot 10^9$$$. Можно показать, что если существует ответ, то он существует и при заданных ограничениях.
Если решений несколько, выведите любое.
4155210 125 20210 3326 6940 2 1 22 2 1 0
YES 5 0 10 NO YES 0 43 33 69 YES 1 0 3 3 1 1
На изображении ниже можно видеть решения из примера. Планируемые дома изображены яркими цветами: розовым и фиолетовым. Существующие дома - тусклыми.
В $$$1$$$ наборе данных первый планируемый дом расположен в точке $$$0$$$, второй - в точке $$$10$$$. Существующий дом расположен в точке $$$5$$$ и находится на расстоянии $$$5$$$ от обеих планируемых домов.

Можно показать, что не существует решения для $$$2$$$ набора данных.

В $$$3$$$ наборе данных планируемые дома расположены в точках $$$33$$$ и $$$69$$$.

Обратите внимание, что в $$$4$$$ тесте оба плана расположены в точке $$$1$$$, где в то же время находится и один из существующих домов, что является корректным расположением.
| Название |
|---|




