Given a rooted tree, define the value of vertex $$$u$$$ in the tree recursively as the MEX$$$^\dagger$$$ of the values of its children. Note that it is only the children, not all of its descendants. In particular, the value of a leaf is $$$0$$$.
Pak Chanek has a rooted tree that initially only contains a single vertex with index $$$1$$$, which is the root. Pak Chanek is going to do $$$q$$$ queries. In the $$$i$$$-th query, Pak Chanek is given an integer $$$x_i$$$. Pak Chanek needs to add a new vertex with index $$$i+1$$$ as the child of vertex $$$x_i$$$. After adding the new vertex, Pak Chanek needs to recalculate the values of all vertices and report the sum of the values of all vertices in the current tree.
$$$^\dagger$$$ The MEX (minimum excluded) of an array is the smallest non-negative integer that does not belong to the array. For example, the MEX of $$$[0,1,1,2,6,7]$$$ is $$$3$$$ and the MEX of $$$[6,9]$$$ is $$$0$$$.
The first line contains a single integer $$$q$$$ ($$$1 \le q \le 3 \cdot 10^5$$$) — the number of operations.
Each of the next $$$q$$$ lines contains a single integer $$$x_i$$$ ($$$1 \leq x_i \leq i$$$) — the description of the $$$i$$$-th query.
For each query, print a line containing an integer representing the sum of the new values of all vertices in the tree after adding the vertex.
7 1 1 3 2 5 2 1
1 1 3 2 4 4 7
8 1 1 1 1 5 6 7 8
1 1 1 1 3 2 4 3
In the first example, the tree after the $$$6$$$-th query will look like this.
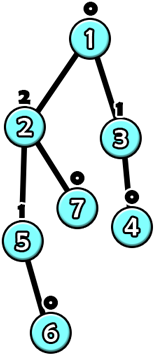
- Vertex $$$7$$$ is a leaf, so its value is $$$0$$$.
- Vertex $$$6$$$ is a leaf, so its value is $$$0$$$.
- Vertex $$$5$$$ only has a child with value $$$0$$$, so its value is $$$1$$$.
- Vertex $$$4$$$ is a leaf, so its value is $$$0$$$.
- Vertex $$$3$$$ only has a child with value $$$0$$$, so its value is $$$1$$$.
- Vertex $$$2$$$ has children with values $$$0$$$ and $$$1$$$, so its value is $$$2$$$.
- Vertex $$$1$$$ has children with values $$$1$$$ and $$$2$$$, so its value is $$$0$$$.
The sum of the values of all vertices is $$$0+0+1+0+1+2+0=4$$$.
| Name |
|---|




