| Codeforces Round 829 (Div. 1) |
|---|
| Finished |
Little Misha goes to the programming club and solves nothing there. It may seem strange, but when you find out that Misha is filming a Minecraft series, everything will fall into place...
Misha is inspired by Manhattan, so he built a city in Minecraft that can be imagined as a table of size $$$n \times m$$$. $$$k$$$ students live in a city, the $$$i$$$-th student lives in the house, located at the intersection of the $$$x_i$$$-th row and the $$$y_i$$$-th column. Also, each student has a degree of his aggressiveness $$$w_i$$$. Since the city turned out to be very large, Misha decided to territorially limit the actions of his series to some square $$$s$$$, which sides are parallel to the coordinate axes. The length of the side of the square should be an integer from $$$1$$$ to $$$\min(n, m)$$$ cells.
According to the plot, the main hero will come to the city and accidentally fall into the square $$$s$$$. Possessing a unique degree of aggressiveness $$$0$$$, he will be able to show his leadership qualities and assemble a team of calm, moderate and aggressive students.
In order for the assembled team to be versatile and close-knit, degrees of aggressiveness of all students of the team must be pairwise distinct and must form a single segment of consecutive integers. Formally, if there exist students with degrees of aggressiveness $$$l, l+1, \ldots, -1, 1, \ldots, r-1, r$$$ inside the square $$$s$$$, where $$$l \le 0 \le r$$$, the main hero will be able to form a team of $$$r-l+1$$$ people (of course, he is included in this team).
Notice, that it is not required to take all students from square $$$s$$$ to the team.
Misha thinks that the team should consist of at least $$$t$$$ people. That is why he is interested, how many squares are there in the table in which the main hero will be able to form a team of at least $$$t$$$ people. Help him to calculate this.
The first line contains four integers $$$n$$$, $$$m$$$, $$$k$$$ and $$$t$$$ ($$$1 \le n, m \le 40\,000$$$, $$$1 \le n \cdot m \le 40\,000$$$, $$$1 \le k \le 10^6$$$, $$$1 \le t \le k + 1$$$) — the number of rows and columns in the table, and the number of students living in the city, respectively.
Each of the following $$$k$$$ lines contains three integers $$$x_i$$$, $$$y_i$$$ and $$$w_i$$$ ($$$1 \le x_i \le n$$$, $$$1 \le y_i \le m$$$, $$$1 \le \lvert w_i \rvert \le 10^9$$$) — the number of row and column, where the $$$i$$$-th student is living, and the degree of his aggressiveness.
Print one integer — the number of ways to choose the square $$$s$$$ in such way that the main hero will be able to form a team of at least $$$t$$$ people.
2 2 1 2 1 1 2
0
2 2 2 2 1 1 1 2 2 2
2
2 2 4 2 1 1 1 1 1 -1 1 2 1 2 2 1
4
- In the first example the main hero will not be able to form a team of more than one person in any square $$$s$$$.
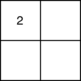 Illustration for the first example.
Illustration for the first example. - In the second example there are two ways to select square $$$s$$$. Both of them are illustrated below. In one of them the main hero will be able to form a team of students with degrees of aggressiveness $$$[0, 1]$$$, and in the another — with degrees of aggressiveness $$$[0, 1, 2]$$$. Notice, that the main hero with degree of aggressiveness $$$0$$$ will be included to the team regardless of the chosen square.
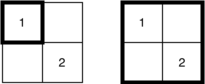 Illustration for the second example.
Illustration for the second example. - In the third example there are four ways to select square $$$s$$$. All of them are illustrated below. The main hero will be able to form a team with degrees of aggressiveness: $$$[-1,0,1]$$$, $$$[0,1]$$$, $$$[0,1]$$$, $$$[-1, 0, 1]$$$, respectively.
 Illustration for the third example.
Illustration for the third example.
| Name |
|---|




