You are given a tree of $$$n$$$ vertices and $$$n - 1$$$ edges. The $$$i$$$-th vertex has an initial weight $$$a_i$$$.
Let the distance $$$d_v(u)$$$ from vertex $$$v$$$ to vertex $$$u$$$ be the number of edges on the path from $$$v$$$ to $$$u$$$. Note that $$$d_v(u) = d_u(v)$$$ and $$$d_v(v) = 0$$$.
Let the weighted distance $$$w_v(u)$$$ from $$$v$$$ to $$$u$$$ be $$$w_v(u) = d_v(u) + a_u$$$. Note that $$$w_v(v) = a_v$$$ and $$$w_v(u) \neq w_u(v)$$$ if $$$a_u \neq a_v$$$.
Analogically to usual distance, let's define the eccentricity $$$e(v)$$$ of vertex $$$v$$$ as the greatest weighted distance from $$$v$$$ to any other vertex (including $$$v$$$ itself), or $$$e(v) = \max\limits_{1 \le u \le n}{w_v(u)}$$$.
Finally, let's define the radius $$$r$$$ of the tree as the minimum eccentricity of any vertex, or $$$r = \min\limits_{1 \le v \le n}{e(v)}$$$.
You need to perform $$$m$$$ queries of the following form:
- $$$v_j$$$ $$$x_j$$$ — assign $$$a_{v_j} = x_j$$$.
After performing each query, print the radius $$$r$$$ of the current tree.
The first line contains the single integer $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — the number of vertices in the tree.
The second line contains $$$n$$$ integers $$$a_1, \dots, a_n$$$ ($$$0 \le a_i \le 10^6$$$) — the initial weights of vertices.
Next $$$n - 1$$$ lines contain edges of tree. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \neq v_i$$$) — the corresponding edge. The given edges form a tree.
The next line contains the single integer $$$m$$$ ($$$1 \le m \le 10^5$$$) — the number of queries.
Next $$$m$$$ lines contain queries — one query per line. The $$$j$$$-th query contains two integers $$$v_j$$$ and $$$x_j$$$ ($$$1 \le v_j \le n$$$; $$$0 \le x_j \le 10^6$$$) — a vertex and it's new weight.
Print $$$m$$$ integers — the radius $$$r$$$ of the tree after performing each query.
6 1 3 3 7 0 1 2 1 1 3 1 4 5 4 4 6 5 4 7 4 0 2 5 5 10 5 5
7 4 5 10 7
After the first query, you have the following tree:

The tree after the second query:
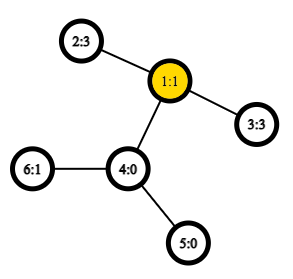
After the third query, the radius $$$r = e(2) = 5$$$:
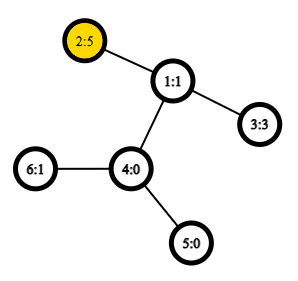
| Name |
|---|




