| Codeforces Round 864 (Div. 2) |
|---|
| Finished |
There is a rectangular maze of size $$$n\times m$$$. Denote $$$(r,c)$$$ as the cell on the $$$r$$$-th row from the top and the $$$c$$$-th column from the left. Two cells are adjacent if they share an edge. A path is a sequence of adjacent empty cells.
Each cell is initially empty. Li Hua can choose some cells (except $$$(x_1, y_1)$$$ and $$$(x_2, y_2)$$$) and place an obstacle in each of them. He wants to know the minimum number of obstacles needed to be placed so that there isn't a path from $$$(x_1, y_1)$$$ to $$$(x_2, y_2)$$$.
Suppose you were Li Hua, please solve this problem.
The first line contains the single integer $$$t$$$ ($$$1 \le t \le 500$$$) — the number of test cases.
The first line of each test case contains two integers $$$n,m$$$ ($$$4\le n,m\le 10^9$$$) — the size of the maze.
The second line of each test case contains four integers $$$x_1,y_1,x_2,y_2$$$ ($$$1\le x_1,x_2\le n, 1\le y_1,y_2\le m$$$) — the coordinates of the start and the end.
It is guaranteed that $$$|x_1-x_2|+|y_1-y_2|\ge 2$$$.
For each test case print the minimum number of obstacles you need to put on the field so that there is no path from $$$(x_1, y_1)$$$ to $$$(x_2, y_2)$$$.
34 42 2 3 36 71 1 2 39 95 1 3 6
4 2 3
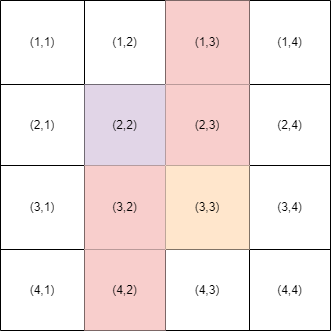
In test case 1, you can put obstacles on $$$(1,3), (2,3), (3,2), (4,2)$$$. Then the path from $$$(2,2)$$$ to $$$(3,3)$$$ will not exist.
 |
| Name |
|---|




