| Codeforces Round 864 (Div. 2) |
|---|
| Finished |
Li Hua has a tree of $$$n$$$ vertices and $$$n-1$$$ edges. The vertices are numbered from $$$1$$$ to $$$n$$$.
A pair of vertices $$$(u,v)$$$ ($$$u < v$$$) is considered cute if exactly one of the following two statements is true:
- $$$u$$$ is the vertex with the minimum index among all vertices on the path $$$(u,v)$$$.
- $$$v$$$ is the vertex with the maximum index among all vertices on the path $$$(u,v)$$$.
There will be $$$m$$$ operations. In each operation, he decides an integer $$$k_j$$$, then inserts a vertex numbered $$$n+j$$$ to the tree, connecting with the vertex numbered $$$k_j$$$.
He wants to calculate the number of cute pairs before operations and after each operation.
Suppose you were Li Hua, please solve this problem.
The first line contains the single integer $$$n$$$ ($$$2\le n\le 2\cdot 10^5$$$) — the number of vertices in the tree.
Next $$$n-1$$$ lines contain the edges of the tree. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1\le u_i,v_i\le n$$$; $$$u_i\ne v_i$$$) — the corresponding edge. The given edges form a tree.
The next line contains the single integer $$$m$$$ ($$$1\le m\le 2\cdot 10^5$$$) — the number of operations.
Next $$$m$$$ lines contain operations — one operation per line. The $$$j$$$-th operation contains one integer $$$k_j$$$ ($$$1\le k_j < n+j$$$) — a vertex.
Print $$$m+1$$$ integers — the number of cute pairs before operations and after each operation.
7 2 1 1 3 1 4 4 6 4 7 6 5 2 5 6
11 15 19
The initial tree is shown in the following picture:
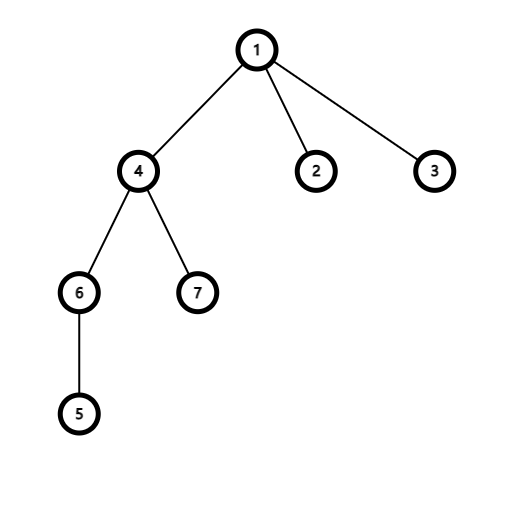 |
There are $$$11$$$ cute pairs — $$$(1,5),(2,3),(2,4),(2,6),(2,7),(3,4),(3,6),(3,7),(4,5),(5,7),(6,7)$$$.
Similarly, we can count the cute pairs after each operation and the result is $$$15$$$ and $$$19$$$.
| Name |
|---|




