| Codeforces Round 868 (Div. 2) |
|---|
| Finished |
You are given a tree consisting of $$$n$$$ vertices and $$$n - 1$$$ edges, and each vertex $$$v$$$ has a counter $$$c(v)$$$ assigned to it.
Initially, there is a chip placed at vertex $$$s$$$ and all counters, except $$$c(s)$$$, are set to $$$0$$$; $$$c(s)$$$ is set to $$$1$$$.
Your goal is to place the chip at vertex $$$t$$$. You can achieve it by a series of moves. Suppose right now the chip is placed at the vertex $$$v$$$. In one move, you do the following:
- choose one of neighbors $$$to$$$ of vertex $$$v$$$ uniformly at random ($$$to$$$ is neighbor of $$$v$$$ if and only if there is an edge $$$\{v, to\}$$$ in the tree);
- move the chip to vertex $$$to$$$ and increase $$$c(to)$$$ by $$$1$$$;
You'll repeat the move above until you reach the vertex $$$t$$$.
For each vertex $$$v$$$ calculate the expected value of $$$c(v)$$$ modulo $$$998\,244\,353$$$.
The first line contains three integers $$$n$$$, $$$s$$$ and $$$t$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$1 \le s, t \le n$$$; $$$s \neq t$$$) — number of vertices in the tree and the starting and finishing vertices.
Next $$$n - 1$$$ lines contain edges of the tree: one edge per line. The $$$i$$$-th line contains two integers $$$u_i$$$ and $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \neq v_i$$$), denoting the edge between the nodes $$$u_i$$$ and $$$v_i$$$.
It's guaranteed that the given edges form a tree.
Print $$$n$$$ numbers: expected values of $$$c(v)$$$ modulo $$$998\,244\,353$$$ for each $$$v$$$ from $$$1$$$ to $$$n$$$.
Formally, let $$$M = 998\,244\,353$$$. It can be shown that the answer can be expressed as an irreducible fraction $$$\frac{p}{q}$$$, where $$$p$$$ and $$$q$$$ are integers and $$$q \not \equiv 0 \pmod{M}$$$. Output the integer equal to $$$p \cdot q^{-1} \bmod M$$$. In other words, output such an integer $$$x$$$ that $$$0 \le x < M$$$ and $$$x \cdot q \equiv p \pmod{M}$$$.
3 1 3 1 2 2 3
2 2 1
4 1 3 1 2 2 3 1 4
4 2 1 2
8 2 6 6 4 6 2 5 4 3 1 2 3 7 4 8 2
1 3 2 0 0 1 0 1
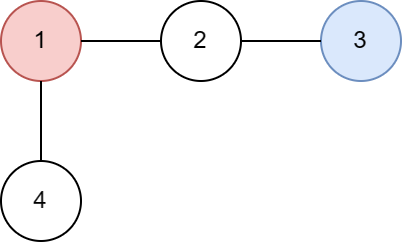
The tree from the first example is shown below:

- $$$P(c(1) = 0) = 0$$$, since $$$c(1)$$$ is set to $$$1$$$ from the start.
- $$$P(c(1) = 1) = \frac{1}{2}$$$, since there is the only one series of moves that leads $$$c(1) = 1$$$. It's $$$1 \rightarrow 2 \rightarrow 3$$$ with probability $$$1 \cdot \frac{1}{2}$$$.
- $$$P(c(1) = 2) = \frac{1}{4}$$$: the only path is $$$1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$$$.
- $$$P(c(1) = 3) = \frac{1}{8}$$$: the only path is $$$1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$$$.
- $$$P(c(1) = i) = \frac{1}{2^i}$$$ in general case.
| Name |
|---|




