| Codeforces Round 871 (Div. 4) |
|---|
| Finished |
In a carnival game, there is a huge pyramid of cans with $$$2023$$$ rows, numbered in a regular pattern as shown.
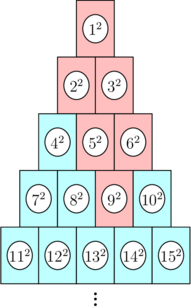
If can $$$9^2$$$ is hit initially, then all cans colored red in the picture above would fall.
You throw a ball at the pyramid, and it hits a single can with number $$$n^2$$$. This causes all cans that are stacked on top of this can to fall (that is, can $$$n^2$$$ falls, then the cans directly above $$$n^2$$$ fall, then the cans directly above those cans, and so on). For example, the picture above shows the cans that would fall if can $$$9^2$$$ is hit.
What is the sum of the numbers on all cans that fall? Recall that $$$n^2 = n \times n$$$.
The first line contains an integer $$$t$$$ ($$$1 \leq t \leq 1000$$$) — the number of test cases.
The only line of each test case contains a single integer $$$n$$$ ($$$1 \leq n \leq 10^6$$$) — it means that the can you hit has label $$$n^2$$$.
For each test case, output a single integer — the sum of the numbers on all cans that fall.
Please note, that the answer for some test cases won't fit into 32-bit integer type, so you should use at least 64-bit integer type in your programming language (like long long for C++). For all valid inputs, the answer will always fit into 64-bit integer type.
1091234561014341000000
156 1 5 10 21 39 46 146 63145186 58116199242129511
The first test case is pictured in the statement. The sum of the numbers that fall is $$$$$$1^2 + 2^2 + 3^2 + 5^2 + 6^2 + 9^2 = 1 + 4 + 9 + 25 + 36 + 81 = 156.$$$$$$
In the second test case, only the can labeled $$$1^2$$$ falls, so the answer is $$$1^2=1$$$.
In the third test case, the cans labeled $$$1^2$$$ and $$$2^2$$$ fall, so the answer is $$$1^2+2^2=1+4=5$$$.
In the fourth test case, the cans labeled $$$1^2$$$ and $$$3^2$$$ fall, so the answer is $$$1^2+3^2=1+9=10$$$.
In the fifth test case, the cans labeled $$$1^2$$$, $$$2^2$$$, and $$$4^2$$$ fall, so the answer is $$$1^2+2^2+4^2=1+4+16=21$$$.
| Name |
|---|




