| Croc Champ 2012 - Final |
|---|
| Finished |
You are given a directed graph G with n vertices and m arcs (multiple arcs and self-loops are allowed). You have to paint each vertex of the graph into one of the k (k ≤ n) colors in such way that for all arcs of the graph leading from a vertex u to vertex v, vertex v is painted with the next color of the color used to paint vertex u.
The colors are numbered cyclically 1 through k. This means that for each color i (i < k) its next color is color i + 1. In addition, the next color of color k is color 1. Note, that if k = 1, then the next color for color 1 is again color 1.
Your task is to find and print the largest possible value of k (k ≤ n) such that it's possible to color G as described above with k colors. Note that you don't necessarily use all the k colors (that is, for each color i there does not necessarily exist a vertex that is colored with color i).
The first line contains two space-separated integers n and m (1 ≤ n, m ≤ 105), denoting the number of vertices and the number of arcs of the given digraph, respectively.
Then m lines follow, each line will contain two space-separated integers ai and bi (1 ≤ ai, bi ≤ n), which means that the i-th arc goes from vertex ai to vertex bi.
Multiple arcs and self-loops are allowed.
Print a single integer — the maximum possible number of the colors that can be used to paint the digraph (i.e. k, as described in the problem statement). Note that the desired value of k must satisfy the inequality 1 ≤ k ≤ n.
4 4
1 2
2 1
3 4
4 3
2
5 2
1 4
2 5
5
4 5
1 2
2 3
3 1
2 4
4 1
3
4 4
1 1
1 2
2 1
1 2
1
For the first example, with k = 2, this picture depicts the two colors (arrows denote the next color of that color).

With k = 2 a possible way to paint the graph is as follows.
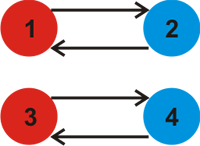
It can be proven that no larger value for k exists for this test case.
For the second example, here's the picture of the k = 5 colors.
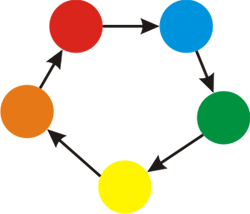
A possible coloring of the graph is:
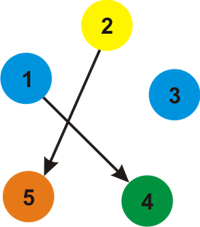
For the third example, here's the picture of the k = 3 colors.
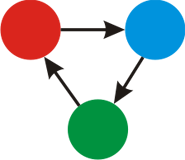
A possible coloring of the graph is:

| Name |
|---|




