This is the hard version of the problem. The differences between the two versions are the constraint on $$$n$$$ and the time limit. You can make hacks only if both versions of the problem are solved.
You are given a tree with $$$n$$$ vertices rooted at vertex $$$1$$$.
For some permutation$$$^\dagger$$$ $$$a$$$ of length $$$n$$$, let $$$f(a)$$$ be the number of pairs of vertices $$$(u, v)$$$ such that $$$a_u < a_{\operatorname{lca}(u, v)} < a_v$$$. Here, $$$\operatorname{lca}(u,v)$$$ denotes the lowest common ancestor of vertices $$$u$$$ and $$$v$$$.
Find the maximum possible value of $$$f(a)$$$ over all permutations $$$a$$$ of length $$$n$$$.
$$$^\dagger$$$ A permutation of length $$$n$$$ is an array consisting of $$$n$$$ distinct integers from $$$1$$$ to $$$n$$$ in arbitrary order. For example, $$$[2,3,1,5,4]$$$ is a permutation, but $$$[1,2,2]$$$ is not a permutation ($$$2$$$ appears twice in the array), and $$$[1,3,4]$$$ is also not a permutation ($$$n=3$$$ but there is $$$4$$$ in the array).
The first line contains a single integer $$$n$$$ ($$$2 \le n \le 10^6$$$).
The second line contains $$$n - 1$$$ integers $$$p_2,p_3,\ldots,p_n$$$ ($$$1 \le p_i < i$$$) indicating that there is an edge between vertices $$$i$$$ and $$$p_i$$$.
Output the maximum value of $$$f(a)$$$.
5 1 1 3 3
4
2 1
0
6 1 2 2 1 5
7
4 1 1 1
2
The tree in the first test:
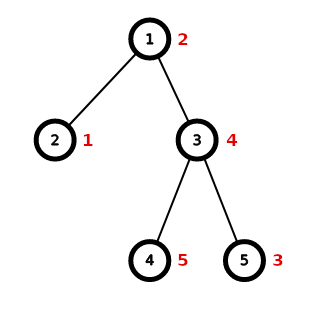
One possible optimal permutation $$$a$$$ is $$$[2, 1, 4, 5, 3]$$$ with $$$4$$$ suitable pairs of vertices:
- $$$(2, 3)$$$, since $$$\operatorname{lca}(2, 3) = 1$$$ and $$$1 < 2 < 4$$$,
- $$$(2, 4)$$$, since $$$\operatorname{lca}(2, 4) = 1$$$ and $$$1 < 2 < 5$$$,
- $$$(2, 5)$$$, since $$$\operatorname{lca}(2, 5) = 1$$$ and $$$1 < 2 < 3$$$,
- $$$(5, 4)$$$, since $$$\operatorname{lca}(5, 4) = 3$$$ and $$$3 < 4 < 5$$$.
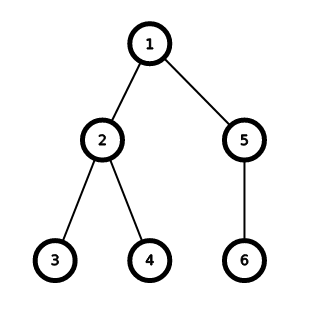
The tree in the third test:
The tree in the fourth test:

| Name |
|---|




