| Codeforces Round 900 (Div. 3) |
|---|
| Finished |
After (finally) qualifying for the IOI 2023, wxhtzdy was very happy, so he decided to do what most competitive programmers do: trying to guess the problems that will be on IOI. During this process, he accidentally made a problem, which he thought was really cool.
You are given a tree (a connected acyclic graph) with $$$n$$$ vertices and $$$n-1$$$ edges. Vertex $$$i$$$ ($$$1 \le i \le n$$$) has a value $$$a_i$$$.
Lets' define $$$g(u, v)$$$ as the bitwise or of the values of all vertices on the shortest path from $$$u$$$ to $$$v$$$. For example, let's say that we want to calculate $$$g(3, 4)$$$, on the tree from the first test case in the example. On the path from $$$3$$$ to $$$4$$$ are vertices $$$3$$$, $$$1$$$, $$$4$$$. Then, $$$g(3, 4) = a_3 \ | \ a_1 \ | \ a_4$$$ (here, $$$|$$$ represents the bitwise OR operation).
Also, you are given $$$q$$$ queries, and each query looks like this:
You are given $$$x$$$ and $$$y$$$. Let's consider all vertices $$$z$$$ such that $$$z$$$ is on the shortest path from $$$x$$$ to $$$y$$$ (inclusive).
Lets define the niceness of a vertex $$$z$$$ as the sum of the number of non-zero bits in $$$g(x, z)$$$ and the number of non-zero bits in $$$g(y, z)$$$. You need to find the maximum niceness among all vertices $$$z$$$ on the shortest path from $$$x$$$ to $$$y$$$.
Since his brain is really tired after solving an output only problem on SIO (he had to do it to qualify for the IOI), he wants your help with this problem.
The first line of input contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
The first line of each test case contains a single integer $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — the number of vertices.
The second line of each test case contains $$$n$$$ positive integers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_v \le 10^9$$$) — the value of each vertex, the $$$i$$$-th integer in this line corresponds to the vertex $$$i$$$.
Following $$$n - 1$$$ lines are the description of a tree.
Each line contains two integers $$$u$$$ and $$$v$$$ ($$$1 \le u, v \le n, u \ne v$$$) — indicating that vertices $$$u$$$ and $$$v$$$ are connected by an edge.
The next line contains a single integer $$$q$$$ ($$$1 \le q \le 10^5$$$) — number of queries.
Following $$$q$$$ lines contain 2 integers $$$x, y$$$ ($$$1 \le x, y \le n$$$) — the vertices $$$x$$$ and $$$y$$$ for each query.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$2 \cdot 10^5$$$.
It is guaranteed that the sum of $$$q$$$ over all test cases does not exceed $$$10^5$$$.
For each test case output $$$q$$$ integers, each of which is the answer to the corresponding query.
341 2 3 41 31 21 431 11 31 437 6 33 12 141 11 21 32 31411 1
2 4 3 6 6 6 6 2
374 7 7 4 10 8 106 13 12 17 41 54 247 52 34 52 569 5 6 2 4 65 12 11 64 31 346 11 44 33 575 1 3 7 5 1 62 15 42 33 47 66 324 27 7
8 6 7 7 6 6 4 7 6 4
176 8 7 2 5 8 72 13 24 34 64 56 741 56 74 51 4
7 7 5 7
The image below shows the tree from the second example, first test case.
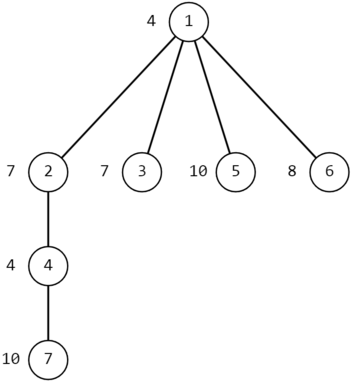 Tree from the second example, first test case
Tree from the second example, first test case In the first query, we have $$$x=7$$$, $$$y=5$$$. The shortest path from $$$7$$$ to $$$5$$$ is $$$7-4-2-1-5$$$.
Let's calculate the niceness of vertex $$$7$$$ on this path. We have $$$g(7,7)=a_7=10=(1010)_2$$$ and $$$g(5,7)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4 \ | \ a_7=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2$$$, so its niceness is equal to $$$2 + 4 = 6$$$.
Now let's calculate the niceness of vertex $$$4$$$ on this path. We have $$$g(7,4)=a_7 \ | \ a_4=10 \ | \ 4=14=(1110)_2$$$ and $$$g(5,4)=a_5 \ | \ a_1 \ | \ a_2 \ | \ a_4=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2$$$, so its niceness is equal to $$$3 + 4 = 7$$$.
Now let's calculate the niceness of vertex $$$2$$$ on this path. We have $$$g(7,2)=a_7 \ | \ a_4 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2$$$ and $$$g(5,2)=a_5 \ | \ a_1 \ | \ a_2=10 \ | \ 4 \ | \ 7=15=(1111)_2$$$, so its niceness is equal to $$$4 + 4 = 8$$$.
Now let's calculate the niceness of vertex $$$1$$$ on this path. We have $$$g(7,1)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1=10 \ | \ 4 \ | \ 7 \ | \ 4=15=(1111)_2$$$ and $$$g(5,1)=a_5 \ | \ a_1=10 \ | \ 4=14=(1110)_2$$$, so its niceness is equal to $$$4 + 3 = 7$$$.
Finally, let's calculate the niceness of vertex $$$5$$$ on this path. We have $$$g(7,5)=a_7 \ | \ a_4 \ | \ a_2 \ | \ a_1 \ | \ a_5=10 \ | \ 4 \ | \ 7 \ | \ 4 \ | \ 10=15=(1111)_2$$$ and $$$g(5,5)=a_5=10=(1010)_2$$$, so its niceness is equal to $$$4 + 2 = 6$$$.
The maximum niceness on this path is at vertex $$$2$$$, and it is $$$8$$$.
| Name |
|---|




