| Codeforces Round 907 (Div. 2) |
|---|
| Finished |
You are given a rooted tree with the root at vertex $$$1$$$, initially consisting of a single vertex. Each vertex has a numerical value, initially set to $$$0$$$. There are also $$$q$$$ queries of two types:
- The first type: add a child vertex with the number $$$sz + 1$$$ to vertex $$$v$$$, where $$$sz$$$ is the current size of the tree. The numerical value of the new vertex will be $$$0$$$.
- The second type: add $$$x$$$ to the numerical values of all vertices in the subtree of vertex $$$v$$$.
After all queries, output the numerical value of all of the vertices in the final tree.
The first line contains a single integer $$$T$$$ ($$$1 \leq T \leq 10^4$$$) — the number of test cases. The descriptions of the test cases follow.
The first line of each test case contains a single integer $$$q$$$ ($$$1 \leq q \leq 5 \cdot 10^5$$$) — the number of queries.
The following $$$q$$$ lines can fall into two cases:
- The first type of query: The $$$i$$$-th line contains two integers $$$t_i$$$ ($$$t_i = 1$$$), $$$v_i$$$. You need to add a child with the number $$$sz + 1$$$ to vertex $$$v_i$$$, where $$$sz$$$ is the current size of the tree. It is guaranteed that $$$1 \leq v_i \leq sz$$$.
- The second type of query: The $$$i$$$-th line contains three integers $$$t_i$$$ ($$$t_i = 2$$$), $$$v_i$$$, $$$x_i$$$ ($$$-10^9 \leq x_i \leq 10^9$$$). You need to add $$$x_i$$$ to all numerical values of vertices in the subtree of $$$v_i$$$. It is guaranteed that $$$1 \leq v_i \leq sz$$$, where $$$sz$$$ is the current size of the tree.
It is guaranteed that the sum of $$$q$$$ across all test cases does not exceed $$$5 \cdot 10^5$$$.
For each test case, output the numerical value of each vertex of the final tree after all queries have been performed.
392 1 31 12 2 11 12 3 21 32 1 41 32 3 252 1 11 12 1 -11 12 1 151 11 12 1 12 1 32 2 10
7 5 8 6 2 1 0 1 4 14 4
In the first case, the final tree with the assigned numerical values will look like this:
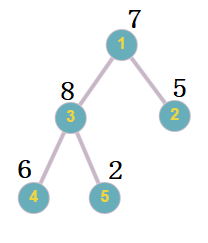 The final tree with the assigned numerical values
The final tree with the assigned numerical values
| Name |
|---|




