| 2023-2024 ICPC, Asia Jakarta Regional Contest (Online Mirror, Unrated, ICPC Rules, Teams Preferred) |
|---|
| Finished |
You are working as a manager in The ICPC Company. In the company building, there are $$$N$$$ computers (numbered from $$$1$$$ to $$$N$$$). There are $$$N - 1$$$ cables, numbered from $$$1$$$ to $$$N - 1$$$, that connect all the computers into a single network. Cable $$$i$$$ connects computer $$$U_i$$$ and $$$V_i$$$. Each cable can be set into emergency mode, where cable $$$i$$$ only transfers data from computer $$$U_i$$$ to computer $$$V_i$$$, but not the other way around. During a disaster, it is mandatory for all cables to be in emergency mode.
Through your research, you discover a new way to determine the vulnerability of a network. You want to add zero or more new cables to the current network such that it is not vulnerable during a disaster. Your network is not vulnerable if and only if there is exactly one permutation of $$$1$$$ to $$$N$$$ such that $$$u$$$ appears before $$$v$$$ in the permutation for all cables that connect computer $$$u$$$ and $$$v$$$. In other words, it should have exactly one topological order.
The following illustration shows examples of not vulnerable networks and vulnerable networks.

For the not vulnerable networks, the only permutation that satisfies the requirement for the networks on the left and on the right are $$$[1, 2, 3]$$$ and $$$[3, 1, 2]$$$, respectively. Meanwhile, for the vulnerable networks, there are $$$2$$$ permutations that satisfy the requirement for the network on the left: $$$[1, 2, 3]$$$ and $$$[3, 1, 2]$$$; while there is no permutation that satisfies the requirement for the network on the right.
You are interested in the minimum number of new cables that should be added to the current network such that it is not vulnerable during a disaster. Furthermore, you want to know, which pairs of computers should be connected by using the minimum number of cables. If there are several ways to connect, you can connect in any way of your choice. Under the given constraints, it can be proven that there exists a way to make the network not vulnerable.
The first line consists of an integer $$$N$$$ ($$$2 \leq N \leq 100\,000$$$).
Each of the next $$$N - 1$$$ lines consists of two integers $$$U_i$$$ $$$V_i$$$ ($$$1 \leq U_i, V_i \leq N$$$). The input edges form a tree.
The first line consists of an integer, representing the minimum number of new cables that should be added to the current network such that it is no longer vulnerable during a disaster. Denote this number as $$$K$$$ and the new cables are numbered from $$$1$$$ to $$$K$$$.
If $$$K$$$ is not $$$0$$$, then output $$$K$$$ lines. Each of the next $$$K$$$ lines consists of two integers $$$A_i$$$ $$$B_i$$$, representing the computers that are connected by the new cable $$$i$$$. During a disaster, new cable $$$i$$$ only transfers data from computer $$$A_i$$$ to computer $$$B_i$$$, but not the other way around. If there exist several solutions, you can output any of them.
3 1 2 3 2
1 3 1
3 1 2 2 3
0
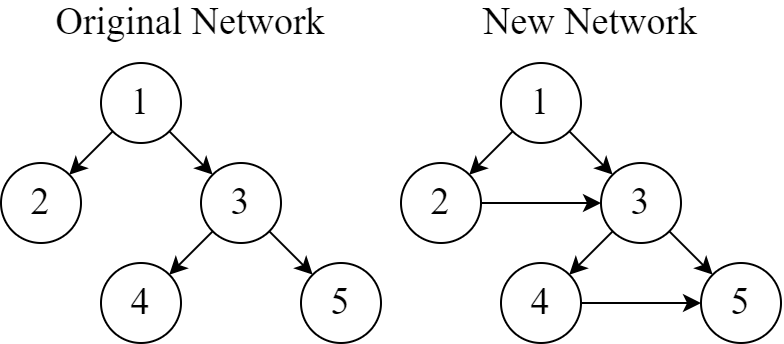
5 1 2 1 3 3 4 3 5
2 2 3 4 5
Explanation for the sample input/output #3
The following illustration shows the original network and the new network with the added cables during a disaster. The only permutation that satisfies the requirement is $$$[1, 2, 3, 4, 5]$$$.
| Name |
|---|




