| Good Bye 2023 |
|---|
| Закончено |
В $$$31$$$ лицее существовало две группы олимпиадников: информатики и математики. Численность информатиков составляла $$$n_1$$$, математиков — $$$n_2$$$. Точно неизвестно кто какой именно группе принадлежал, но известно, что между некоторыми парами людей существовали дружественные связи (причем они могли образовываться как между парой людей одной группы, так и двух различных).
Связи были настолько крепкими, что даже если убрать одного человека, а вместе с ним убрать все его дружественные связи, то любая пара людей всё равно оставалась знакома либо напрямую, либо через общих приятелей.
$$$^{\dagger}$$$ Более формально, два человека $$$(x, y)$$$ знакомы в следующем случае: найдутся такие люди $$$a_1, a_2, \ldots,a_n$$$ ($$$1 \le a_i \le n_1 + n_2$$$), что одновременно выполняются следующие условия:
$$$\bullet$$$ Человек $$$x$$$ напрямую знаком с $$$a_1$$$.
$$$\bullet$$$ Человек $$$a_n$$$ напрямую знаком с $$$y$$$.
$$$\bullet$$$ Человек $$$a_i$$$ напрямую знаком с $$$a_{i + 1}$$$ для любого ($$$1 \le i \le n - 1$$$).
Преподаватели были недовольны тем, что информатики дружат с математиками и наоборот, и поэтому они решили разделить школьников на две группы таким образом, чтобы выполнялось два условия:
$$$\bullet$$$ В группе информатиков было $$$n_1$$$ человек, а в группе математиков — $$$n_2$$$ человек.
$$$\bullet$$$ Любая пара информатиков должна быть знакома (допускается знакомство при участии общих знакомых, которые обязаны быть из той же группы, что и люди из этой пары), тоже самое должно выполняться и для математиков.
Помогите им разрешить эту задачу и найдите, кто к какой группе относится.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит три целых числа $$$n_1$$$, $$$n_2$$$ и $$$m$$$ ($$$1 \le n_1, n_2 \le 2000$$$, $$$1 \le m \le 5000$$$). $$$n_1$$$, $$$n_2$$$ являются размерами двух групп, описанных в задаче, $$$m$$$ — количество дружественных связей изначально.
В следующих $$$m$$$ строках дано описание дружественных связей: в $$$i$$$-й ($$$1 \le i \le m$$$) из них дана пара чисел $$$(a, b)$$$, которая означает, что человек с номером $$$a$$$ дружит с человеком с номером $$$b$$$ (и обратно).
Гарантируется, что для каждого набора входных данных все дружественные связи различные.
Гарантируется, что сумма $$$n_1 + n_2$$$ по всем наборам входных данных не превосходит $$$2000$$$, а сумма $$$m$$$ по всем наборам входных данных не превосходит $$$5000$$$.
Также гарантируется, что для каждого набора входных данных ответ существует.
Для каждого набора входных данных выведите две строки.
В первой строке выведите $$$n_1$$$ различных чисел $$$a_i$$$ ($$$1 \le a_i \le n_1 + n_2$$$) — люди, принадлежащие первой группе.
Во второй строке выведите $$$n_2$$$ различных чисел $$$b_i$$$ ($$$1 \le b_i \le n_1 + n_2$$$) — люди, принадлежащие второй группе.
Все числа должны быть различные.
Если существует несколько вариантов ответа, выведите любой.
31 2 32 31 31 21 4 72 53 42 41 23 54 51 53 3 71 21 62 32 53 44 54 6
3 1 2 5 1 2 3 4 4 5 6 1 2 3
Рассмотрим третий набор входных данных. Разделение на группы выглядит следующим образом:
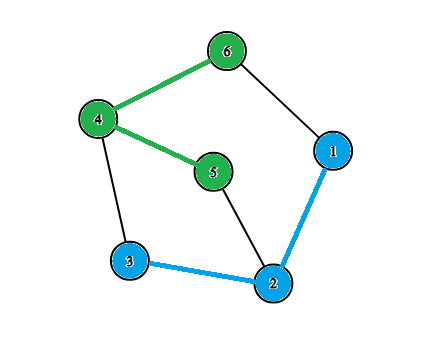
Рассмотрим все пары информатиков и то, как они знакомы:
Пары $$$(4, 5), (4, 6)$$$ знакомы напрямую.
Пара $$$(5, 6)$$$ знакома через информатика с номером $$$4$$$.
Рассмотрим все пары математиков и то, как они знакомы:
Пары $$$(1, 2), (2, 3)$$$ знакомы напрямую.
Пара $$$(1, 3)$$$ знакома через математика с номером $$$2$$$.
Получаем, что любая пара людей, принадлежащих одной группе, знакомы друг с другом, а значит разбиение на две группы верное.
| Название |
|---|




