| Codeforces Round 123 (Div. 2) |
|---|
| Finished |
An oriented weighted forest is an acyclic weighted digraph in which from each vertex at most one edge goes.
The root of vertex v of an oriented weighted forest is a vertex from which no edge goes and which can be reached from vertex v moving along the edges of the weighted oriented forest. We denote the root of vertex v as root(v).
The depth of vertex v is the sum of weights of paths passing from the vertex v to its root. Let's denote the depth of the vertex v as depth(v).
Let's consider the process of constructing a weighted directed forest. Initially, the forest does not contain vertices. Vertices are added sequentially one by one. Overall, there are n performed operations of adding. The i-th (i > 0) adding operation is described by a set of numbers (k, v1, x1, v2, x2, ... , vk, xk) and means that we should add vertex number i and k edges to the graph: an edge from vertex root(v1) to vertex i with weight depth(v1) + x1, an edge from vertex root(v2) to vertex i with weight depth(v2) + x2 and so on. If k = 0, then only vertex i is added to the graph, there are no added edges.
Your task is like this: given the operations of adding vertices, calculate the sum of the weights of all edges of the forest, resulting after the application of all defined operations, modulo 1000000007 (109 + 7).
The first line contains a single integer n (1 ≤ n ≤ 105) — the number of operations of adding a vertex.
Next n lines contain descriptions of the operations, the i-th line contains the description of the operation of adding the i-th vertex in the following format: the first number of a line is an integer k (0 ≤ k ≤ i - 1), then follow 2k space-separated integers: v1, x1, v2, x2, ... , vk, xk (1 ≤ vj ≤ i - 1, |xj| ≤ 109).
The operations are given in the order, in which they should be applied to the graph. It is guaranteed that sum k of all operations does not exceed 105, also that applying operations of adding vertexes does not result in loops and multiple edges.
Print a single number — the sum of weights of all edges of the resulting graph modulo 1000000007 (109 + 7).
6
0
0
1 2 1
2 1 5 2 2
1 1 2
1 3 4
30
5
0
1 1 5
0
0
2 3 1 4 3
9
Conside the first sample:
- Vertex 1 is added. k = 0, thus no edges are added.
- Vertex 2 is added. k = 0, thus no edges are added.
- Vertex 3 is added. k = 1. v1 = 2, x1 = 1. Edge from vertex root(2) = 2 to vertex 3 with weight depth(2) + x1 = 0 + 1 = 1 is added.
- Vertex 4 is added. k = 2. v1 = 1, x1 = 5. Edge from vertex root(1) = 1 to vertex 4 with weight depth(1) + x1 = 0 + 5 = 5 is added. v2 = 2, x2 = 2. Edge from vertex root(2) = 3 to vertex 4 with weight depth(2) + x1 = 1 + 2 = 3 is added.
- Vertex 5 is added. k = 1. v1 = 1, x1 = 2. Edge from vertex root(1) = 4 to vertex 5 with weight depth(1) + x1 = 5 + 2 = 7 is added.
- Vertex 6 is added. k = 1. v1 = 3, x1 = 4. Edge from vertex root(3) = 5 to vertex 6 with weight depth(3) + x1 = 10 + 4 = 14 is added.
The resulting graph is shown on the pictore below: 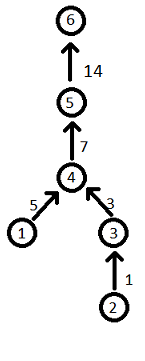
| Name |
|---|




