| Codeforces Global Round 25 |
|---|
| Finished |
You are given an undirected connected simple graph with $$$n$$$ nodes and $$$m$$$ edges, where edge $$$i$$$ connects node $$$u_i$$$ and $$$v_i$$$, with two positive parameters $$$a_i$$$ and $$$b_i$$$ attached to it. Additionally, you are also given an integer $$$k$$$.
A non-negative array $$$x$$$ with size $$$m$$$ is called a $$$k$$$-spanning-tree generator if it satisfies the following:
- Consider the undirected multigraph with $$$n$$$ nodes where edge $$$i$$$ is cloned $$$x_i$$$ times (i.e. there are $$$x_i$$$ edges connecting $$$u_i$$$ and $$$v_i$$$). It is possible to partition the edges of this graph into $$$k$$$ spanning trees, where each edge belongs to exactly one spanning tree$$$^\dagger$$$.
The cost of such array $$$x$$$ is defined as $$$\sum_{i = 1}^m a_i x_i^2 + b_i x_i$$$. Find the minimum cost of a $$$k$$$-spanning-tree generator.
$$$^\dagger$$$ A spanning tree of a (multi)graph is a subset of the graph's edges that form a tree connecting all vertices of the graph.
Each test contains multiple test cases. The first line contains an integer $$$t$$$ ($$$1 \le t \le 500$$$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains three integers $$$n$$$, $$$m$$$, and $$$k$$$ ($$$2 \le n \le 50, n - 1 \le m \le \min(50, \frac{n(n - 1)}{2}), 1 \le k \le 10^7$$$) — the number of nodes in the graph, the number of edges in the graph, and the parameter for the $$$k$$$-spanning-tree generator.
Each of the next $$$m$$$ lines of each test case contains four integers $$$u_i$$$, $$$v_i$$$, $$$a_i$$$, and $$$b_i$$$ ($$$1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le a_i, b_i \le 1000$$$) — the endpoints of the edge $$$i$$$ and its two parameters. It is guaranteed that the graph is simple and connected.
It is guaranteed that the sum of $$$n^2$$$ and the sum of $$$m^2$$$ over all test cases does not exceed $$$2500$$$.
For each test case, output a single integer: the minimum cost of a $$$k$$$-spanning-tree generator.
45 5 14 3 5 52 1 5 72 4 6 25 3 3 52 5 2 95 5 34 3 5 52 1 5 72 4 6 25 3 3 52 5 2 92 1 100000001 2 1000 100010 15 107 1 7 65 8 6 64 8 2 24 3 10 910 8 3 44 6 6 15 4 1 39 3 4 38 3 9 97 5 10 32 1 3 46 1 6 42 5 7 310 7 2 18 2 6 8
38 191 100000010000000000 2722
In the first test case, a valid $$$1$$$-spanning-tree generator is $$$x = [1, 1, 1, 1, 0]$$$, as indicated by the following figure. The cost of this generator is $$$(1^2 \cdot 5 + 1 \cdot 5) + (1^2 \cdot 5 + 1 \cdot 7) + (1^2 \cdot 6 + 1 \cdot 2) + (1^2 \cdot 3 + 1 \cdot 5) + (0^2 \cdot 4 + 0 \cdot 9) = 38$$$. It can be proven that no other generator has a lower cost.
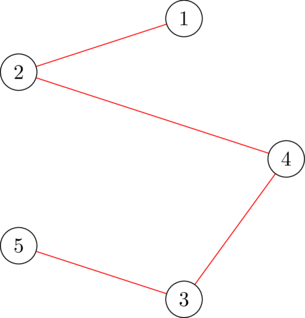 The $$$1$$$-spanning-tree partition of $$$x = [1, 1, 1, 1, 0]$$$
The $$$1$$$-spanning-tree partition of $$$x = [1, 1, 1, 1, 0]$$$ In the second test case, a valid $$$3$$$-spanning-tree generator is $$$x = [2, 3, 2, 2, 3]$$$, as indicated by the following figure. The cost of this generator is $$$(2^2 \cdot 5 + 2 \cdot 5) + (3^2 \cdot 5 + 3 \cdot 7) + (2^2 \cdot 6 + 2 \cdot 2) + (2^2 \cdot 3 + 2 \cdot 5) + (3^2 \cdot 4 + 3 \cdot 9) = 191$$$. It can be proven that no other generator has a lower cost.
 The $$$3$$$-spanning-tree partition of $$$x = [2, 3, 2, 2, 3]$$$
The $$$3$$$-spanning-tree partition of $$$x = [2, 3, 2, 2, 3]$$$
| Name |
|---|




