| Codeforces Round 949 (Div. 2) |
|---|
| Finished |
Turtle just received $$$n$$$ segments and a sequence $$$a_1, a_2, \ldots, a_n$$$. The $$$i$$$-th segment is $$$[l_i, r_i]$$$.
Turtle will create an undirected graph $$$G$$$. If segment $$$i$$$ and segment $$$j$$$ intersect, then Turtle will add an undirected edge between $$$i$$$ and $$$j$$$ with a weight of $$$|a_i - a_j|$$$, for every $$$i \ne j$$$.
Turtle wants you to calculate the sum of the weights of the edges of the minimum spanning tree of the graph $$$G$$$, or report that the graph $$$G$$$ has no spanning tree.
We say two segments $$$[l_1, r_1]$$$ and $$$[l_2, r_2]$$$ intersect if and only if $$$\max(l_1, l_2) \le \min(r_1, r_2)$$$.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^5$$$). The description of the test cases follows.
The first line of each test case contains a single integer $$$n$$$ ($$$2 \le n \le 5 \cdot 10^5$$$) — the number of segments.
The $$$i$$$-th of the following $$$n$$$ lines contains three integers $$$l_i, r_i, a_i$$$ ($$$1 \le l_i \le r_i \le 10^9, 1 \le a_i \le 10^9$$$) — the $$$i$$$-th segment and the $$$i$$$-th element of the sequence.
It is guaranteed that the sum of $$$n$$$ over all test cases does not exceed $$$5 \cdot 10^5$$$.
For each test case, output a single integer — the sum of the weights of the edges of the minimum spanning tree of the graph $$$G$$$. If the graph $$$G$$$ has no spanning tree, output $$$-1$$$.
451 7 32 4 63 5 56 7 93 4 452 7 31 3 64 5 56 7 91 1 441 4 31 2 13 4 51 4 431 3 12 3 34 5 8
9 13 4 -1
In the first test case, the graph $$$G$$$ is as follows:

One of the minimum spanning trees of $$$G$$$ is as follows:

The sum of the weights of the edges of the minimum spanning tree is $$$9$$$.
In the second test case, the graph $$$G$$$ is as follows:

$$$G$$$ is already a tree, and the sum of the weights of the tree is $$$13$$$.
In the third test case, the graph $$$G$$$ is as follows:
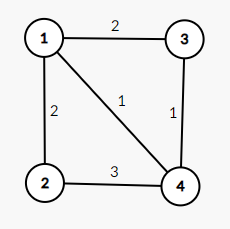
In the fourth test case, the graph $$$G$$$ is as follows:

It's easy to see that $$$G$$$ is not connected, so $$$G$$$ has no spanning tree.
| Name |
|---|




