| Codeforces Round 175 (Div. 2) |
|---|
| Finished |
Permutation p is an ordered set of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. We'll denote the i-th element of permutation p as pi. We'll call number n the size or the length of permutation p1, p2, ..., pn.
We'll call position i (1 ≤ i ≤ n) in permutation p1, p2, ..., pn good, if |p[i] - i| = 1. Count the number of permutations of size n with exactly k good positions. Print the answer modulo 1000000007 (109 + 7).
The single line contains two space-separated integers n and k (1 ≤ n ≤ 1000, 0 ≤ k ≤ n).
Print the number of permutations of length n with exactly k good positions modulo 1000000007 (109 + 7).
1 0
1
2 1
0
3 2
4
4 1
6
7 4
328
The only permutation of size 1 has 0 good positions.
Permutation (1, 2) has 0 good positions, and permutation (2, 1) has 2 positions.
Permutations of size 3:
- (1, 2, 3) — 0 positions
-
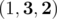 — 2 positions
— 2 positions -
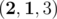 — 2 positions
— 2 positions -
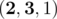 — 2 positions
— 2 positions -
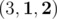 — 2 positions
— 2 positions - (3, 2, 1) — 0 positions
| Name |
|---|




